구문 분석

어휘 분석을 통해 소스 코드가 토큰(token)들의 스트림으로 변환되었다면, 컴파일러의 다음 주요 단계는 구문 분석(Syntax Analysis) 입니다. 구문 분석기는 이 토큰 스트림을 입력으로 받아 프로그램의 문법적 구조를 파악하고, 이를 보통 파스 트리(Parse Tree) 또는 구문 트리(Syntax Tree) 형태로 표현합니다. 이 과정을 파싱(Parsing) 이라고도 합니다.

어휘 분석에서 토큰의 패턴을 정의하기 위해 정규 표현식(Regular Expression)을 사용했던 것처럼, 구문 분석에서는 프로그램의 구조, 즉 문장들이나 구문 요소들이 어떻게 결합되어 올바른 프로그램을 형성하는지를 정의하기 위해 문맥 자유 문법(Context-Free Grammar, CFG)을 사용합니다.

문맥 자유 문법 (Context-Free Grammar, CFG)

정규 표현식과 유한 오토마타는 어휘 단위(토큰)를 인식하는 데는 강력하지만, 중첩(nesting) 구조나 재귀적인 구조를 표현하는 데는 한계가 있습니다. 예를 들어, 괄호의 짝 맞추기, begin-end 블록 구조, 또는 재귀적인 수식 구조 등은 정규 언어만으로는 완벽하게 표현하기 어렵습니다. 이러한 2차원적인, 계층적인 구조를 표현하기 위해서는 정규 표현식보다 표현력이 더 강한 문맥 자유 문법이 필요합니다.

회문(Palindrome) 은 문맥 자유 문법으로 표현할 수 있지만 정규 언어로는 표현할 수 없는 대표적인 예입니다. 회문은 앞에서부터 읽으나 뒤에서부터 읽으나 동일한 문자열을 말합니다 (예: "madam", "racecar", 또는 알파벳 [math]\displaystyle{ \{0, 1\} }[/math] 상에서는 "0110", "101"). 회문을 정의하는 문맥 자유 문법은 다음과 같이 재귀적으로 정의될 수 있습니다:

• 기본 케이스 (Bases):
  • [math]\displaystyle{ P \rightarrow \epsilon }[/math] (빈 문자열은 회문이다)
  • [math]\displaystyle{ P \rightarrow 0 }[/math] ('0' 자체는 회문이다)
  • [math]\displaystyle{ P \rightarrow 1 }[/math] ('1' 자체는 회문이다)
• 귀납적 단계 (Induction): 만약 문자열 [math]\displaystyle{ w }[/math]가 회문이라면, 다음도 회문입니다:
  • [math]\displaystyle{ P \rightarrow 0P0 }[/math] ([math]\displaystyle{ w }[/math]의 양쪽에 '0'을 붙인 [math]\displaystyle{ 0w0 }[/math]도 회문이다)
  • [math]\displaystyle{ P \rightarrow 1P1 }[/math] ([math]\displaystyle{ w }[/math]의 양쪽에 '1'을 붙인 [math]\displaystyle{ 1w1 }[/math]도 회문이다)

모든 문맥 자유 문법은 이처럼 재귀적인 정의를 통해 언어를 생성합니다.

문맥 자유 문법의 형식적 정의

문맥 자유 문법 [math]\displaystyle{ G }[/math]는 다음 네 가지 구성요소의 튜플 [math]\displaystyle{ (V, T, S, P) }[/math]로 정의됩니다:

• [math]\displaystyle{ V }[/math]: 논터미널(Non-terminal) 기호들의 유한한 집합입니다. 논터미널은 문법 규칙을 통해 더 작은 단위로 확장될 수 있는 구문 변수(syntactic variable)를 나타냅니다 (예: Expression, Statement, NounPhrase).
• [math]\displaystyle{ T }[/math]: 터미널(Terminal) 기호들의 유한한 집합입니다. 터미널은 문법의 가장 기본적인 단위로, 더 이상 확장되지 않는 기호들입니다. 어휘 분석기가 생성하는 토큰들이 여기에 해당합니다 (예: id, number, +, if). [math]\displaystyle{ V }[/math]와 [math]\displaystyle{ T }[/math]는 서로소 집합입니다 ([math]\displaystyle{ V \cap T = \emptyset }[/math]).
• [math]\displaystyle{ S }[/math]: [math]\displaystyle{ V }[/math]에 속하는 특별한 논터미널 기호로, 시작 심볼(Start Symbol) 이라고 합니다. 문법은 이 시작 심볼로부터 유도를 시작합니다.
• [math]\displaystyle{ P }[/math]: 생성 규칙(Production rule) 들의 유한한 집합입니다. 각 생성 규칙은 [math]\displaystyle{ A \rightarrow \alpha }[/math] 형태를 가집니다.
  • [math]\displaystyle{ A \in V }[/math]는 논터미널입니다.
  • [math]\displaystyle{ \alpha \in (V \cup T)^* }[/math]는 터미널과 논터미널 기호들의 문자열입니다 ([math]\displaystyle{ \alpha }[/math]는 빈 문자열 [math]\displaystyle{ \epsilon }[/math]일 수도 있습니다).
  • 이 규칙은 "논터미널 [math]\displaystyle{ A }[/math]는 문자열 [math]\displaystyle{ \alpha }[/math]로 대체될(파생될) 수 있다"라고 읽습니다.

유도 (Derivation)

문맥 자유 문법 [math]\displaystyle{ G = (V, T, S, P) }[/math]가 주어졌을 때, 문자열이 이 문법에 의해 생성될 수 있는지를 확인하는 과정을 유도(Derivation) 라고 합니다. 유도는 생성 규칙을 반복적으로 적용하여 시작 심볼로부터 특정 문자열을 만들어내는 과정입니다.

• 직접 유도 (Direct Derivation, [math]\displaystyle{ \Rightarrow }[/math]): 만약 [math]\displaystyle{ \alpha A \beta }[/math]가 터미널과 논터미널로 이루어진 문자열이고 ([math]\displaystyle{ A \in V }[/math], [math]\displaystyle{ \alpha, \beta \in (V \cup T)^* }[/math]), [math]\displaystyle{ A \rightarrow \gamma }[/math]가 [math]\displaystyle{ G }[/math]의 생성 규칙 중 하나라면, [math]\displaystyle{ \alpha A \beta }[/math]는 [math]\displaystyle{ \alpha \gamma \beta }[/math]를 직접 유도한다고 하며, [math]\displaystyle{ \alpha A \beta \Rightarrow \alpha \gamma \beta }[/math]로 표기합니다. "문맥 자유"라는 이름은 논터미널 [math]\displaystyle{ A }[/math]를 [math]\displaystyle{ \gamma }[/math]로 대체할 때 [math]\displaystyle{ A }[/math]의 주변 문맥(context)인 [math]\displaystyle{ \alpha }[/math]와 [math]\displaystyle{ \beta }[/math]에 영향을 받지 않는다는 의미에서 유래합니다.

• 유도 클로저 ([math]\displaystyle{ \Rightarrow^* }[/math]): [math]\displaystyle{ \Rightarrow^* }[/math]는 0번 이상의 직접 유도 과정을 나타내는 관계입니다.
  • 기본 케이스: 임의의 문자열 [math]\displaystyle{ \alpha \in (V \cup T)^* }[/math]에 대해, [math]\displaystyle{ \alpha \Rightarrow^* \alpha }[/math] 입니다 (0번 유도).
  • 귀납적 케이스: 만약 [math]\displaystyle{ \alpha \Rightarrow^* \beta }[/math]이고 [math]\displaystyle{ \beta \Rightarrow \gamma }[/math]이면, [math]\displaystyle{ \alpha \Rightarrow^* \gamma }[/math] 입니다.

어떤 문자열 [math]\displaystyle{ w }[/math]가 문법 [math]\displaystyle{ G }[/math]에 포함되는지 확인하려면, 시작 심볼 [math]\displaystyle{ S }[/math]로부터 [math]\displaystyle{ S \Rightarrow^* w }[/math]가 가능한지 보면 됩니다. 파싱(Parsing)은 이러한 유도 과정을 역으로 수행하여, 주어진 터미널 문자열(토큰 스트림)이 시작 심볼로부터 어떻게 유도되었는지를 찾아내는 과정입니다.

• 문장 형식 (Sentential Forms): 문법 [math]\displaystyle{ G=(V, T, S, P) }[/math]에서 시작 심볼 [math]\displaystyle{ S }[/math]로부터 유도될 수 있는 모든 문자열 [math]\displaystyle{ \alpha \in (V \cup T)^* }[/math] (즉, [math]\displaystyle{ S \Rightarrow^* \alpha }[/math]를 만족하는 [math]\displaystyle{ \alpha }[/math])를 문장 형식이라고 합니다. 문장 형식은 터미널과 논터미널을 모두 포함할 수 있습니다.

• 문장 (Sentence): 문장 형식 중에서 논터미널을 전혀 포함하지 않는, 즉 터미널 기호로만 이루어진 문자열을 해당 문법의 문장이라고 합니다.

• 문법의 언어 (Language of a Grammar): 문법 [math]\displaystyle{ G }[/math]가 생성하는 언어 [math]\displaystyle{ L(G) }[/math]는 [math]\displaystyle{ G }[/math]의 모든 문장들의 집합입니다. 즉, [math]\displaystyle{ L(G) = \{ w \in T^* \mid S \Rightarrow^* w \} }[/math] 입니다.

유도 방식: 좌측 최단 유도와 우측 최단 유도

하나의 문장 형식에서 여러 개의 논터미널이 존재할 경우, 어떤 논터미널을 먼저 확장할지에 대한 선택이 필요합니다. 이를 위해 표준적인 유도 방식이 정의되어 있습니다:

• 좌측 최단 유도 (Leftmost Derivation, [math]\displaystyle{ \Rightarrow_l }[/math] 또는 [math]\displaystyle{ \Rightarrow_{lm} }[/math]):

각 유도 단계에서 항상 가장 왼쪽에 있는 논터미널 을 선택하여 생성 규칙을 적용합니다. 만약 [math]\displaystyle{ S \Rightarrow_l^* \alpha }[/math]이면, [math]\displaystyle{ \alpha }[/math]를 좌측 문장 형식(left sentential form) 이라고 합니다.

• 우측 최단 유도 (Rightmost Derivation, [math]\displaystyle{ \Rightarrow_r }[/math] 또는 [math]\displaystyle{ \Rightarrow_{rm} }[/math]):

각 유도 단계에서 항상 가장 오른쪽에 있는 논터미널 을 선택하여 생성 규칙을 적용합니다. 만약 [math]\displaystyle{ S \Rightarrow_r^* \alpha }[/math]이면, [math]\displaystyle{ \alpha }[/math]를 우측 문장 형식(right sentential form) 이라고 합니다. 우측 최단 유도는 특히 LR 파서와 같이 상향식(bottom-up) 파싱에서 유도 과정을 역순으로 구성하는 데 사용됩니다.

어떤 문법에 대해 주어진 문자열이 그 문법에 속한다면, 그 문자열에 대한 좌측 최단 유도와 우측 최단 유도가 각각 존재합니다 (때로는 유일하게 존재).

파스 트리 (Parse Tree)

파스 트리(Parse Tree) 또는 구체적인 구문 트리(Concrete Syntax Tree, CST)는 문맥 자유 문법으로부터 특정 문자열이 어떻게 유도되었는지를 시각적으로 보여주는 트리 형태의 표현입니다. 파스 트리는 유도 과정에서 논터미널이 생성 규칙에 의해 대체되는 순서의 변화는 무시하고, 어떤 규칙이 어떤 부분에 적용되었는지만을 나타냅니다. 즉, 동일한 규칙들을 사용하여 동일한 문자열을 유도했다면, 유도 순서(예: 좌측 최단 또는 우측 최단)에 관계없이 동일한 파스 트리가 생성됩니다.

파스 트리는 다음과 같은 속성을 가집니다:

• 루트 노드(Root Node): 문법의 시작 심볼 [math]\displaystyle{ S }[/math]로 레이블링됩니다.
• 내부 노드(Internal Node): 논터미널 기호 [math]\displaystyle{ A \in V }[/math]로 레이블링됩니다.
• 단말 노드(Leaf Node): 터미널 기호 [math]\displaystyle{ a \in T }[/math] 또는 빈 문자열 [math]\displaystyle{ \epsilon }[/math]으로 레이블링됩니다.
• 생성 규칙과의 관계: 만약 어떤 내부 노드가 논터미널 [math]\displaystyle{ A }[/math]로 레이블링되어 있고, 그 자식 노드들이 왼쪽에서 오른쪽으로 [math]\displaystyle{ X_1, X_2, \dots, X_k }[/math]로 레이블링되어 있다면, [math]\displaystyle{ A \rightarrow X_1 X_2 \dots X_k }[/math]는 반드시 문법 [math]\displaystyle{ P }[/math]에 포함된 생성 규칙이어야 합니다. (만약 [math]\displaystyle{ A \rightarrow \epsilon }[/math] 규칙이 적용되었다면, [math]\displaystyle{ A }[/math] 노드는 [math]\displaystyle{ \epsilon }[/math]으로 레이블링된 단일 자식 노드를 가집니다.)

파스 트리의 단말 노드들을 왼쪽에서 오른쪽으로 순서대로 읽으면 원래 유도된 문자열(문장)을 얻을 수 있습니다.

예시: 문법 [math]\displaystyle{ E \rightarrow E + E \mid E \star E \mid (E) \mid \text{id} }[/math] 에 대해 문자열 id + id를 유도하는 한 가지 방법은 [math]\displaystyle{ E \Rightarrow E+E \Rightarrow \text{id}+E \Rightarrow \text{id}+\text{id} }[/math] 입니다. 또 다른 유도 순서로 [math]\displaystyle{ E \Rightarrow E+E \Rightarrow E+\text{id} \Rightarrow \text{id}+\text{id} }[/math]가 있을 수 있습니다. 하지만 이 두 유도 과정은 동일한 파스 트리를 생성합니다.

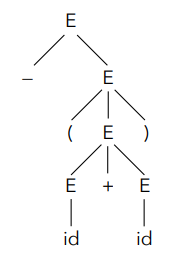
만약 문법이 [math]\displaystyle{ E \rightarrow -E \mid (E) \mid E+E \mid E \star E \mid \text{id} }[/math] 이고 문자열이 -(id+id) 라면, 그 파스 트리는 다음과 같은 구조를 가질 수 있습니다:

1. 루트 E는 자식으로 -와 다른 E (E1)를 가집니다.
2. E1은 자식으로 (, 다른 E (E2), )를 가집니다.
3. E2는 자식으로 또 다른 E (E3), +, 그리고 E (E4)를 가집니다.
4. E3과 E4는 각각 자식으로 id를 가집니다.

모호성 (Ambiguity)

하나의 문법이 특정 문장에 대해 두 개 이상의 서로 다른 파스 트리 를 생성할 수 있다면, 그 문법을 모호한 문법(ambiguous grammar) 이라고 합니다. 모호성은 다음과 같은 경우에도 나타납니다:

• 하나의 문장에 대해 두 개 이상의 서로 다른 좌측 최단 유도가 존재하는 경우.
• 하나의 문장에 대해 두 개 이상의 서로 다른 우측 최단 유도가 존재하는 경우.

프로그래밍 언어에서 모호성은 심각한 문제를 일으킵니다. 왜냐하면 파스 트리는 프로그램의 의미를 결정하는 데 중요한 역할을 하는데, 파스 트리가 여러 개 존재한다는 것은 프로그램의 의미가 여러 가지로 해석될 수 있다는 뜻이기 때문입니다. 예를 들어, 3 + 4 * 5라는 수식은 [math]\displaystyle{ (3+4) \star 5 }[/math]로 해석될 수도 있고, [math]\displaystyle{ 3 + (4 \star 5) }[/math]로 해석될 수도 있습니다. 문법이 모호하면 컴파일러는 어떤 파스 트리를 선택해야 할지 결정할 수 없습니다.

모호성 제거 (Eliminating Ambiguity)

일반적으로 모호한 문법은 모호하지 않은 문법으로 변경하여 사용해야 합니다. 모호성을 제거하는 일반적인 방법은 없지만, 프로그래밍 언어에서 자주 나타나는 모호성(특히 수식 문법에서의 모호성)은 다음과 같은 기법을 사용하여 해결할 수 있습니다: 1. 우선순위(Precedence) 명시: 연산자들 사이에 우선순위를 부여합니다. 예를 들어, 곱셈(\star)이 덧셈(+)보다 높은 우선순위를 갖도록 문법을 계층적으로 설계합니다. 1 + 2 * 3은 항상 [math]\displaystyle{ 1 + (2 \star 3) }[/math]으로 해석되도록 합니다. 이를 위해 보통 다음과 같이 여러 레벨의 논터미널을 도입합니다: [math]\displaystyle{ E \rightarrow E + T \mid T }[/math] (덧셈/뺄셈 레벨, 가장 낮은 우선순위) [math]\displaystyle{ T \rightarrow T \star F \mid F }[/math] (곱셈/나눗셈 레벨) [math]\displaystyle{ F \rightarrow (E) \mid \text{id} }[/math] (괄호/기본 요소 레벨, 가장 높은 우선순위)

2. 결합성(Associativity) 명시: 동일한 우선순위를 갖는 연산자들이 연속해서 나타날 때, 왼쪽부터 결합할지(left-associative) 오른쪽부터 결합할지(right-associative)를 문법에 명시합니다. 예를 들어, 덧셈(+)과 곱셈(\star)은 보통 왼쪽 결합성을 가집니다. 1 + 2 + 3은 항상 [math]\displaystyle{ (1 + 2) + 3 }[/math]으로 해석되도록 합니다.

• • 왼쪽 결합성 은 보통 [math]\displaystyle{ A \rightarrow A \text{ op } B \mid B }[/math] 형태의 좌측 재귀(left-recursive) 생성 규칙으로 표현됩니다 (예: [math]\displaystyle{ E \rightarrow E + T \mid T }[/math]).
  • 오른쪽 결합성 은 보통 [math]\displaystyle{ A \rightarrow B \text{ op } A \mid B }[/math] 형태의 우측 재귀(right-recursive) 생성 규칙으로 표현됩니다 (예: 할당 연산자 =는 종종 오른쪽 결합성을 가집니다. [math]\displaystyle{ S \rightarrow \text{id} = S \mid \dots }[/math]).

위의 수정된 문법 [math]\displaystyle{ E \rightarrow E + T \mid T }[/math], [math]\displaystyle{ T \rightarrow T \star F \mid F }[/math], [math]\displaystyle{ F \rightarrow (E) \mid \text{id} }[/math]는 *가 +보다 높은 우선순위를 가지며, 두 연산자 모두 왼쪽 결합성을 갖도록 모호성을 제거한 예입니다.

파서가 처리하기 어려운 문법 변형

파싱 알고리즘(특히 하향식 파서)은 특정 형태의 문법 규칙을 직접 처리하기 어려워하는 경우가 있습니다. 이를 해결하기 위해 문법을 변형하는 기법들이 사용됩니다.

좌측 재귀 제거 (Eliminating Left-Recursion)

생성 규칙이 [math]\displaystyle{ A \rightarrow A\alpha \mid \beta }[/math]와 같이 자기 자신을 가장 왼쪽에서 직접 또는 간접적으로 호출하는 형태를 좌측 재귀(left-recursion) 라고 합니다. (예: [math]\displaystyle{ E \rightarrow E+T }[/math]) 하향식 파서(top-down parser)는 좌측 재귀 규칙을 만나면 무한 루프에 빠질 수 있습니다.

직접적인 좌측 재귀 [math]\displaystyle{ A \rightarrow A\alpha \mid \beta }[/math] (여기서 [math]\displaystyle{ \beta }[/math]는 [math]\displaystyle{ A }[/math]로 시작하지 않음)는 다음과 같은 규칙들로 변형하여 제거할 수 있습니다:

• [math]\displaystyle{ A \rightarrow \beta A' }[/math]
• [math]\displaystyle{ A' \rightarrow \alpha A' \mid \epsilon }[/math]

예를 들어, [math]\displaystyle{ E \rightarrow E+T \mid T }[/math]는 다음과 같이 변형됩니다:

• [math]\displaystyle{ E \rightarrow T E' }[/math]
• [math]\displaystyle{ E' \rightarrow +T E' \mid \epsilon }[/math]

이 변환은 문법이 생성하는 언어를 변경하지 않으면서 좌측 재귀를 우측 재귀 형태로 바꿉니다.

좌측 인수분해 (Left Factoring)

하나의 논터미널에 대해 두 개 이상의 생성 규칙이 동일한 접두사(prefix)로 시작하는 경우 (예: [math]\displaystyle{ S \rightarrow \text{if } E \text{ then } S \text{ else } S }[/math] 와 [math]\displaystyle{ S \rightarrow \text{if } E \text{ then } S }[/math]), 하향식 파서는 어떤 규칙을 선택해야 할지 결정하기 위해 추가적인 입력을 더 읽어야 합니다. 좌측 인수분해(Left Factoring) 는 이러한 공통 접두사를 분리하여 파서가 결정을 쉽게 내릴 수 있도록 문법을 변형하는 기법입니다.

일반적으로 [math]\displaystyle{ A \rightarrow \alpha \beta_1 \mid \alpha \beta_2 }[/math] 형태의 규칙들은 다음과 같이 변형됩니다:

• [math]\displaystyle{ A \rightarrow \alpha A' }[/math]
• [math]\displaystyle{ A' \rightarrow \beta_1 \mid \beta_2 }[/math]

예를 들어, 다음 두 규칙은:

• [math]\displaystyle{ S \rightarrow \text{if } E \text{ then } S \text{ else } S }[/math]
• [math]\displaystyle{ S \rightarrow \text{if } E \text{ then } S }[/math]

다음과 같이 좌측 인수분해 될 수 있습니다:

• [math]\displaystyle{ S \rightarrow \text{if } E \text{ then } S X }[/math]
• [math]\displaystyle{ X \rightarrow \text{else } S \mid \epsilon }[/math]

여기서 [math]\displaystyle{ X }[/math]는 새로운 논터미널입니다.

문맥 자유 문법으로 표현하기 어려운 언어 구조들 (Non-Context-Free Language Constructs)

문맥 자유 문법은 많은 프로그래밍 언어의 구문 구조를 효과적으로 표현할 수 있지만, 모든 언어적 제약을 다룰 수 있는 것은 아닙니다. CFG의 표현력에는 한계가 있으며, 다음과 같은 경우들은 일반적으로 CFG만으로는 검사하기 어렵고, 주로 의미 분석(semantic analysis) 단계에서 처리됩니다.

• 사례 1: 변수 선언 후 사용 확인

언어 [math]\displaystyle{ L_1 = \{ wcw \mid w \in (a|b)^* \} }[/math] 를 생각해봅시다. 이는 [math]\displaystyle{ w }[/math]라는 문자열이 선언되고, 나중에 정확히 동일한 [math]\displaystyle{ w }[/math]가 사용되는 상황을 모델링할 수 있습니다 (예: int x; ... x = 5;). 문맥 자유 문법은 [math]\displaystyle{ w }[/math]의 첫 번째 발생과 두 번째 발생이 동일한 문자열임을 보장하기 어렵습니다. 즉, "식별자는 사용하기 전에 선언되어야 한다"는 규칙은 CFG로 표현하기 힘듭니다.

• 사례 2: 함수 호출 시 인자 개수 일치 확인

언어 [math]\displaystyle{ L_2 = \{ a^n b^m c^n d^m \mid n \ge 1, m \ge 1 \} }[/math] 와 같은 구조는 함수의 정의와 호출에서 인자의 개수나 타입이 일치하는지를 검사하는 상황과 유사합니다. 즉, [math]\displaystyle{ a }[/math]의 개수와 [math]\displaystyle{ c }[/math]의 개수가 같고, [math]\displaystyle{ b }[/math]의 개수와 [math]\displaystyle{ d }[/math]의 개수가 같아야 하는 제약은 CFG로 표현할 수 없습니다.

이러한 속성들은 "문맥에 민감한(context-sensitive)" 정보에 해당하며, 파싱 단계 이후의 의미 분석 단계에서 심볼 테이블(symbol table) 등의 자료구조를 활용하여 검사하는 것이 일반적입니다.