구문 분석: Difference between revisions
No edit summary |
No edit summary |
||
| Line 318: | Line 318: | ||
* 만약 <math>\text{FIRST}(\alpha) \cap \text{FIRST}(\beta) \neq \emptyset</math> 인 두 규칙 <math>A \rightarrow \alpha</math> 와 <math>A \rightarrow \beta</math> 가 있다면, 문법은 예측 파싱으로 파싱될 수 없습니다. | * 만약 <math>\text{FIRST}(\alpha) \cap \text{FIRST}(\beta) \neq \emptyset</math> 인 두 규칙 <math>A \rightarrow \alpha</math> 와 <math>A \rightarrow \beta</math> 가 있다면, 문법은 예측 파싱으로 파싱될 수 없습니다. | ||
* 이러한 예측 파싱으로 파싱 가능한 문법을 '''LL(1) 문법'''이라고 합니다 (Left-to-right scan, Leftmost derivation, 1-symbol lookahead). | * 이러한 예측 파싱으로 파싱 가능한 문법을 '''LL(1) 문법'''이라고 합니다 (Left-to-right scan, Leftmost derivation, 1-symbol lookahead). | ||
== 상향식 파싱 (Bottom-Up Parsing) == | |||
지금까지 파스 트리의 루트(시작 심볼)에서부터 시작하여 단말 노드로 내려가면서 트리를 구축하는 하향식 파싱 방법에 대해 알아보았습니다. 이제는 정반대의 접근 방식인 '''상향식 파싱(Bottom-Up Parsing)'''에 대해 자세히 살펴봅시다. | |||
상향식 파싱은 입력 문자열(즉, 파스 트리의 단말 노드들)에서 시작하여, 이들을 점차적으로 문법 규칙에 따라 결합하고 상위의 논터미널로 대체(축약, reduce)해 나갑니다. 이 과정을 반복하여 최종적으로 트리의 루트 노드인 시작 심볼에 도달하는 방식으로 파스 트리를 구축합니다. 이 과정은 마치 오른쪽 최단 유도(Rightmost Derivation)를 역순으로 만들어가는 것과 같습니다. 예를 들어, <code>id*id</code>라는 입력이 주어졌을 때, 상향식 파서는 <math>\text{id}*\text{id} \Rightarrow F*\text{id} \Rightarrow T*\text{id} \Rightarrow T*F \Rightarrow T \Rightarrow E</math> 와 같이 오른쪽 최단 유도의 역순으로 진행됩니다. | |||
상향식 파싱은 일반적으로 하향식 파싱보다 더 넓은 범위의 문법을 처리할 수 있어 강력한 파싱 전략으로 알려져 있습니다. | |||
=== 핸들 (Handle) === | |||
상향식 파싱의 핵심 과정은 현재까지 스캔한 입력 문자열의 어느 부분을 어떤 문법 규칙을 사용해 논터미널로 축약(reduce)할 것인지 결정하는 것입니다. 이때, 축약의 대상이 되는 부분 문자열을 '''핸들(Handle)'''이라고 부릅니다. 보다 정확하게, 핸들은 다음 두 가지 조건을 만족합니다: | |||
# 현재 처리 중인 오른쪽 문장 형식(right sentential form) 내의 특정 부분 문자열이어야 하며, 이 부분 문자열은 어떤 생성 규칙 <math>A \rightarrow \beta</math>의 우변 <math>\beta</math>와 정확히 일치해야 합니다. | |||
# 이 부분 문자열 <math>\beta</math>를 해당 규칙의 좌변인 논터미널 <math>A</math>로 치환(축약)했을 때, 그 결과가 여전히 오른쪽 최단 유도의 한 단계 이전 형태가 되어야 합니다. 즉, 시작 심볼로부터 원래의 오른쪽 문장 형식으로 도달하는 오른쪽 최단 유도 과정 중에 나타나는 유효한 단계여야 합니다. | |||
상향식 파서의 기본 작업은 "핸들을 찾고, 그 핸들을 해당하는 논터미널로 축약하는" 과정을 반복하는 것입니다. 예를 들어, 문장 형식 <math>T*id</math> 에서 <code>id</code>는 <math>F \rightarrow \text{id}</math> 규칙의 핸들이 될 수 있습니다. 이를 <math>F</math>로 축약하면 <math>T*F</math>가 됩니다. | |||
=== LR 파싱 === | |||
LR 파싱은 가장 대표적이고 강력한 상향식 파싱 기법 중 하나입니다. '''LR'''이라는 이름은 다음을 의미합니다: | |||
* '''L''': 입력 문자열을 '''L'''eft-to-right (왼쪽에서 오른쪽으로) 스캔합니다. | |||
* '''R''': 오른쪽 최단 유도(Rightmost derivation)를 역순으로 구성합니다. | |||
* (k): 다음 입력 토큰을 최대 '''k'''개까지 미리 보고(lookahead) 파싱 결정을 내립니다. (실제로는 k=1인 LR(1) 파서가 가장 일반적으로 사용되며, 여기서 k는 보통 생략되거나 1로 간주됩니다.) | |||
LR 파서는 결정적 유한 오토마타(DFA)를 사용하여 언제 쉬프트(shift)하고 언제 축약(reduce)할지, 특히 핸들을 어떻게 인식할지를 결정합니다. | |||
==== LR 파싱 개요 ==== | |||
LR 파서는 주로 다음과 같은 구성요소로 이루어집니다: | |||
* '''입력 버퍼:''' 아직 처리되지 않은 나머지 토큰 스트림을 저장합니다. 입력의 끝은 특수 기호 <math>$</math>로 표시됩니다. | |||
* '''스택:''' 파싱 과정에서 상태(state)들을 저장합니다. 각 상태는 지금까지 처리한 입력 부분에 대한 정보를 요약합니다. | |||
* '''파싱 테이블:''' 현재 스택의 최상단 상태와 다음 입력 토큰(lookahead)을 기반으로 파서가 수행할 행동(action)과 다음 상태(goto)를 결정하는 데 사용됩니다. | |||
파서는 현재 스택의 최상단 상태와 미리 본 입력 토큰을 참조하여 파싱 테이블에서 다음 행동을 결정합니다. 주요 행동은 다음과 같습니다: | |||
* '''쉬프트 (Shift s):''' 현재 입력 토큰을 스택으로 옮기고, 파서는 상태 <math>s</math>로 전이합니다. 입력 포인터는 다음 토큰으로 이동합니다. | |||
* '''축약 (Reduce <math>A \rightarrow \beta</math>):''' 스택의 최상단에 핸들 <math>\beta</math>가 인식되었음을 의미합니다. 스택에서 <math>\beta</math>에 해당하는 심볼 수만큼 (정확히는 <math>2 \times |\beta|</math> 개의 상태와 심볼, 또는 상태만을 관리한다면 <math>|\beta|</math> 개의 상태) pop 합니다. 그 후, 스택의 새로운 최상단 상태와 규칙의 좌변인 논터미널 <math>A</math>를 사용하여 GOTO 테이블을 참조, 다음 상태를 결정하여 <math>A</math>와 함께 그 상태를 스택에 push 합니다. | |||
* '''수락 (Accept):''' 입력 문자열 전체가 성공적으로 파싱되어 시작 심볼로 축약되었음을 의미합니다. 파싱이 성공적으로 종료됩니다. | |||
* '''오류 (Error):''' 파싱 테이블에 유효한 행동이 없는 경우 구문 오류가 발생했음을 의미합니다. | |||
==== LR 파싱 테이블과 핸들 인식 ==== | |||
LR 파싱 테이블은 DFA(LR 오토마톤)로부터 생성됩니다. 이 DFA의 각 상태는 현재까지 가능한 파싱 상태를 나타내며, 주로 "LR 아이템"이라는 특별한 생성 규칙 형태로 표현됩니다. | |||
테이블은 두 부분으로 구성됩니다: | |||
* '''ACTION[상태, 터미널]:''' 현재 스택 top의 '상태'와 다음 입력 '터미널'에 따라 수행할 동작 (shift, reduce, accept, error)을 지정합니다. | |||
* '''GOTO[상태, 논터미널]:''' reduce 동작 후, 스택 top의 '상태'와 방금 축약되어 생성된 '논터미널'에 따라 전이할 다음 상태를 지정합니다. | |||
예를 들어, 아래는 표현식 문법에 대한 LR 파싱 테이블의 일부입니다 (s는 shift, r은 reduce, 숫자는 상태 또는 규칙 번호, acc는 accept, g는 goto). | |||
{| class="wikitable" | |||
|+ LR 파싱 테이블 예시 (SLR) | |||
! 상태 !! id !! + !! * !! ( !! ) !! $ !! '''E''' !! '''T''' !! '''F''' | |||
|- | |||
! 0 || s5 || || || s4 || || || g1 || g2 || g3 | |||
|- | |||
! 1 || || s6 || || || || acc || || || | |||
|- | |||
! 2 || || r2(<math>E \rightarrow T</math>) || s7 || || r2(<math>E \rightarrow T</math>) || r2(<math>E \rightarrow T</math>) || || || | |||
|- | |||
! ... || ... || ... || ... || ... || ... || ... || ... || ... || ... | |||
|} | |||
만약 현재 상태가 2이고 다음 입력이 <code>+</code>이면, 테이블은 <math>E \rightarrow T</math> 규칙(규칙 2번)으로 축약(r2)하라고 지시합니다. 만약 다음 입력이 <code>*</code>이면, s7 (7번 상태로 쉬프트)을 지시합니다. | |||
==== LR 파싱 과정 (스택에 상태 저장) ==== | |||
실제 LR 파서는 스택에 (상태, 심볼) 쌍 대신 주로 상태 번호만을 저장하여 효율성을 높입니다. 심볼은 암묵적으로 각 상태와 연관됩니다. | |||
다음은 <code>id * id$</code> 입력에 대한 LR 파싱 과정의 예시입니다 (위 테이블 및 표현식 문법 기준). | |||
{| class="wikitable" | |||
|+ <code>id * id$</code> LR 파싱 과정 (스택에 상태 저장) | |||
! 스택 (상태) !! (암묵적) 심볼 스택 !! 입력 !! 행동 | |||
|- | |||
| <code>0</code> || <code>$</code> || <code>id * id$</code> || ACTION[0,id]=s5 (shift 5) | |||
|- | |||
| <code>0 5</code> || <code>$id</code> || <code>* id$</code> || ACTION[5,*]=r6 (<math>F \rightarrow \text{id}</math>), GOTO[0,F]=g3 | |||
|- | |||
| <code>0 3</code> || <code>$F</code> || <code>* id$</code> || ACTION[3,*]=r4 (<math>T \rightarrow F</math>), GOTO[0,T]=g2 | |||
|- | |||
| <code>0 2</code> || <code>$T</code> || <code>* id$</code> || ACTION[2,*]=s7 (shift 7) | |||
|- | |||
| <code>0 2 7</code> || <code>$T*</code> || <code>id$</code> || ACTION[7,id]=s5 (shift 5) | |||
|- | |||
| <code>0 2 7 5</code> || <code>$T*id</code> || <code>$</code> || ACTION[5,$]=r6 (<math>F \rightarrow \text{id}</math>), GOTO[7,F]=g10 | |||
|- | |||
| <code>0 2 7 10</code> || <code>$T*F</code> || <code>$</code> || ACTION[10,$]=r3 (<math>T \rightarrow T*F</math>), GOTO[0,T]=g2 | |||
|- | |||
| <code>0 2</code> || <code>$T</code> || <code>$</code> || ACTION[2,$]=r2 (<math>E \rightarrow T</math>), GOTO[0,E]=g1 | |||
|- | |||
| <code>0 1</code> || <code>$E</code> || <code>$</code> || ACTION[1,$]=acc (accept) | |||
|} | |||
=== LR 파서의 종류 및 생성 === | |||
LR 파서는 얼마나 많은 lookahead 토큰을 사용하는지와 파싱 테이블을 구축하는 방식에 따라 LR(0), SLR(1), LALR(1), LR(1) 등으로 나뉩니다. | |||
==== LR(0) 아이템과 LR(0) 오토마톤 ==== | |||
* '''LR(0) 아이템:''' 생성 규칙의 우변에 점(dot, <math>\cdot</math>)을 추가하여 파싱 진행 상태를 나타냅니다. 예를 들어, <math>A \rightarrow \cdot XYZ, A \rightarrow X \cdot YZ, A \rightarrow XY \cdot Z, A \rightarrow XYZ \cdot</math> 와 같습니다. | |||
* '''CLOSURE 연산:''' 아이템 집합 <math>I</math>에 대해, <math>I</math>의 모든 아이템과, <math>A \rightarrow \alpha \cdot B \beta</math> 형태의 아이템이 있을 때 모든 <math>B \rightarrow \cdot \gamma</math> 규칙을 추가하여 아이템 집합을 확장합니다. 이 과정을 더 이상 아이템이 추가되지 않을 때까지 반복합니다. | |||
* '''GOTO(I, X) 연산:''' 아이템 집합 <math>I</math>와 문법 기호 <math>X</math>에 대해, <math>I</math> 내의 <math>A \rightarrow \alpha \cdot X \beta</math> 아이템들에서 점을 <math>X</math> 다음으로 옮긴 <math>A \rightarrow \alpha X \cdot \beta</math> 형태의 아이템들의 집합에 CLOSURE를 적용하여 새로운 상태(아이템 집합)를 만듭니다. | |||
* '''LR(0) 오토마톤:''' 문법을 확장한 규칙 <math>S' \rightarrow S</math>의 아이템 <math>S' \rightarrow \cdot S</math>에 CLOSURE를 적용한 것을 초기 상태로 하여, GOTO 연산을 통해 모든 가능한 상태와 전이를 찾아 DFA를 구성합니다. | |||
==== LR(0) 및 SLR 파싱 테이블 구축 ==== | |||
* '''LR(0) 테이블:''' | |||
* GOTO(I, a) = J (a는 터미널)이면, ACTION[I, a] = shift J. | |||
* GOTO(I, A) = J (A는 논터미널)이면, GOTO[I, A] = J. | |||
* <math>S' \rightarrow S \cdot</math> 이 <math>I</math>에 있으면, ACTION[I, $] = accept. | |||
* <math>A \rightarrow \alpha \cdot</math> (단, <math>A \neq S'</math>)가 <math>I</math>에 있으면, '''모든''' 터미널 <math>t</math> 및 <math>$</math>에 대해 ACTION[I, t] = reduce <math>A \rightarrow \alpha</math>. 이 마지막 조건 때문에 LR(0)는 충돌이 발생하기 쉽습니다. | |||
* '''SLR(Simple LR) 테이블:''' LR(0)의 reduce 행동을 개선합니다. <math>A \rightarrow \alpha \cdot</math> 이 <math>I</math>에 있을 때, <math>\text{FOLLOW}(A)</math>에 속하는 각 터미널 <math>t</math>에 대해서만 ACTION[I, t] = reduce <math>A \rightarrow \alpha</math>를 추가합니다. 이를 통해 많은 불필요한 충돌을 줄일 수 있습니다. | |||
==== 파싱 테이블 충돌 (Conflicts) ==== | |||
파싱 테이블의 한 셀에 두 가지 이상의 행동이 정의되면 충돌이 발생합니다. | |||
* '''쉬프트/리듀스 충돌 (Shift/Reduce Conflict):''' 동일한 상태와 입력 토큰에 대해 쉬프트와 리듀스 행동 중 하나를 선택해야 하는 경우. | |||
* '''리듀스/리듀스 충돌 (Reduce/Reduce Conflict):''' 동일한 상태와 입력 토큰에 대해 두 가지 이상의 다른 생성 규칙으로 리듀스할 수 있는 경우. | |||
충돌이 없는 LR(0) 문법이나 SLR 문법은 해당 파싱 방법으로 파싱이 가능합니다. 하지만 SLR로도 해결되지 않는 충돌이 존재합니다. | |||
==== LALR(1) 및 LR(1) 파서 ==== | |||
더 강력한 LR 파싱 방법으로 LR(1)과 LALR(1)이 있습니다. | |||
* '''LR(1) 파서:''' LR(0) 아이템에 추가적으로 하나의 lookahead 터미널을 포함하는 LR(1) 아이템 (<math>(A \rightarrow \alpha \cdot \beta, a)</math>)을 사용합니다. 이는 축약 결정을 내릴 때 lookahead 정보를 활용하여 매우 강력한 파싱 능력을 제공하지만, 생성되는 상태의 수가 매우 많아질 수 있다는 단점이 있습니다. | |||
* '''LALR(1) (Look-Ahead LR) 파서:''' LR(1) 오토마톤의 상태들 중 핵심 LR(0) 아이템 부분은 같지만 lookahead만 다른 상태들을 병합하여 상태 수를 줄인 방식입니다. LR(1)보다는 약간 약하지만 SLR보다는 훨씬 강력하며, 파싱 테이블의 크기가 LR(0) 오토마톤과 동일하여 실용적으로 널리 사용됩니다 (예: Yacc, Bison). | |||
상향식 파싱은 이처럼 다양한 기법과 정교한 테이블 구축 과정을 통해 강력한 파싱 능력을 제공하며, 많은 프로그래밍 언어 컴파일러에서 채택하고 있는 방식입니다. | |||
Revision as of 01:12, 29 May 2025
이전 페이지: Compiler
지난 어휘 분석 문서에서는 소스 코드를 의미 있는 가장 작은 단위인 토큰(token)들의 연속으로 변환하는 과정을 다뤘습니다. 이번 Lecture 3에서는 컴파일러의 다음 주요 단계인 구문 분석(Syntax Analysis)에 대해 다룹니다.
가장 먼저, 구문 구조를 정의하는 핵심 도구인 문맥 자유 문법(Context-Free Grammar, CFG)의 개념과 형식적 정의, 그리고 CFG로부터 문자열이 생성되는 과정인 유도(Derivation)에 대해 배웁니다. 또한, 유도 과정을 시각적으로 표현하는 파스 트리와 프로그래밍 언어에서 문제를 일으킬 수 있는 모호성(Ambiguity) 및 이를 해결하는 방법을 다룹니다. 마지막으로, 실제 파서가 문법을 효과적으로 처리할 수 있도록 문법을 변형하는 기법들(좌측 재귀 제거, 좌측 인수분해)과 CFG만으로는 표현하기 어려운 언어 구조들에 대해서도 살펴볼 것입니다.
이러한 문법적 기초를 다진 후, 대표적인 파싱 전략 중 하나인 하향식 파싱(Top-Down Parsing) 방법, 특히 예측 파싱(Predictive Parsing)과 이를 구현하는 데 필요한 FIRST와 FOLLOW 집합, 그리고 파싱 테이블 구축 방법에 대해 자세히 알아보겠습니다.
문맥 자유 문법 (Context-Free Grammar, CFG)
정규 표현식과 유한 오토마타는 어휘 단위(토큰)를 인식하는 데는 강력하지만, 중첩(nesting) 구조나 재귀적인 구조를 표현하는 데는 한계가 있습니다. 예를 들어, 괄호의 짝 맞추기, begin-end 블록 구조, 또는 재귀적인 수식 구조 등은 정규 언어만으로는 완벽하게 표현하기 어렵습니다. 이러한 2차원적인, 계층적인 구조를 표현하기 위해서는 정규 표현식보다 표현력이 더 강한 문맥 자유 문법이 필요합니다.
회문(Palindrome) 은 문맥 자유 문법으로 표현할 수 있지만 정규 언어로는 표현할 수 없는 대표적인 예입니다. 회문은 앞에서부터 읽으나 뒤에서부터 읽으나 동일한 문자열을 말합니다 (예: "madam", "racecar", 또는 알파벳 [math]\displaystyle{ \{0, 1\} }[/math] 상에서는 "0110", "101"). 회문을 정의하는 문맥 자유 문법은 다음과 같이 재귀적으로 정의될 수 있습니다:
- 기본 케이스 (Bases):
- [math]\displaystyle{ P \rightarrow \epsilon }[/math] (빈 문자열은 회문이다)
- [math]\displaystyle{ P \rightarrow 0 }[/math] ('0' 자체는 회문이다)
- [math]\displaystyle{ P \rightarrow 1 }[/math] ('1' 자체는 회문이다)
- 귀납적 단계 (Induction): 만약 문자열 [math]\displaystyle{ w }[/math]가 회문이라면, 다음도 회문입니다:
- [math]\displaystyle{ P \rightarrow 0P0 }[/math] ([math]\displaystyle{ w }[/math]의 양쪽에 '0'을 붙인 [math]\displaystyle{ 0w0 }[/math]도 회문이다)
- [math]\displaystyle{ P \rightarrow 1P1 }[/math] ([math]\displaystyle{ w }[/math]의 양쪽에 '1'을 붙인 [math]\displaystyle{ 1w1 }[/math]도 회문이다)
모든 문맥 자유 문법은 이처럼 재귀적인 정의를 통해 언어를 생성합니다.
문맥 자유 문법의 형식적 정의
문맥 자유 문법 [math]\displaystyle{ G }[/math]는 다음 네 가지 구성요소의 튜플 [math]\displaystyle{ (V, T, S, P) }[/math]로 정의됩니다:
- [math]\displaystyle{ V }[/math]: 논터미널(Non-terminal) 기호들의 유한한 집합입니다. 논터미널은 문법 규칙을 통해 더 작은 단위로 확장될 수 있는 구문 변수(syntactic variable)를 나타냅니다 (예:
Expression,Statement,NounPhrase). - [math]\displaystyle{ T }[/math]: 터미널(Terminal) 기호들의 유한한 집합입니다. 터미널은 문법의 가장 기본적인 단위로, 더 이상 확장되지 않는 기호들입니다. 어휘 분석기가 생성하는 토큰들이 여기에 해당합니다 (예:
id,number,+,if). [math]\displaystyle{ V }[/math]와 [math]\displaystyle{ T }[/math]는 서로소 집합입니다 ([math]\displaystyle{ V \cap T = \emptyset }[/math]). - [math]\displaystyle{ S }[/math]: [math]\displaystyle{ V }[/math]에 속하는 특별한 논터미널 기호로, 시작 심볼(Start Symbol) 이라고 합니다. 문법은 이 시작 심볼로부터 유도를 시작합니다.
- [math]\displaystyle{ P }[/math]: 생성 규칙(Production rule) 들의 유한한 집합입니다. 각 생성 규칙은 [math]\displaystyle{ A \rightarrow \alpha }[/math] 형태를 가집니다.
- [math]\displaystyle{ A \in V }[/math]는 논터미널입니다.
- [math]\displaystyle{ \alpha \in (V \cup T)^* }[/math]는 터미널과 논터미널 기호들의 문자열입니다 ([math]\displaystyle{ \alpha }[/math]는 빈 문자열 [math]\displaystyle{ \epsilon }[/math]일 수도 있습니다).
- 이 규칙은 "논터미널 [math]\displaystyle{ A }[/math]는 문자열 [math]\displaystyle{ \alpha }[/math]로 대체될(파생될) 수 있다"라고 읽습니다.
유도 (Derivation)
문맥 자유 문법 [math]\displaystyle{ G = (V, T, S, P) }[/math]가 주어졌을 때, 문자열이 이 문법에 의해 생성될 수 있는지를 확인하는 과정을 유도(Derivation) 라고 합니다. 유도는 생성 규칙을 반복적으로 적용하여 시작 심볼로부터 특정 문자열을 만들어내는 과정입니다.
- 직접 유도 (Direct Derivation, [math]\displaystyle{ \Rightarrow }[/math]): 만약 [math]\displaystyle{ \alpha A \beta }[/math]가 터미널과 논터미널로 이루어진 문자열이고 ([math]\displaystyle{ A \in V }[/math], [math]\displaystyle{ \alpha, \beta \in (V \cup T)^* }[/math]), [math]\displaystyle{ A \rightarrow \gamma }[/math]가 [math]\displaystyle{ G }[/math]의 생성 규칙 중 하나라면, [math]\displaystyle{ \alpha A \beta }[/math]는 [math]\displaystyle{ \alpha \gamma \beta }[/math]를 직접 유도한다고 하며, [math]\displaystyle{ \alpha A \beta \Rightarrow \alpha \gamma \beta }[/math]로 표기합니다. "문맥 자유"라는 이름은 논터미널 [math]\displaystyle{ A }[/math]를 [math]\displaystyle{ \gamma }[/math]로 대체할 때 [math]\displaystyle{ A }[/math]의 주변 문맥(context)인 [math]\displaystyle{ \alpha }[/math]와 [math]\displaystyle{ \beta }[/math]에 영향을 받지 않는다는 의미에서 유래합니다.
- 유도 클로저 ([math]\displaystyle{ \Rightarrow^* }[/math]): [math]\displaystyle{ \Rightarrow^* }[/math]는 0번 이상의 직접 유도 과정을 나타내는 관계입니다.
- 기본 케이스: 임의의 문자열 [math]\displaystyle{ \alpha \in (V \cup T)^* }[/math]에 대해, [math]\displaystyle{ \alpha \Rightarrow^* \alpha }[/math] 입니다(0번 유도).
- 귀납적 케이스: 만약 [math]\displaystyle{ \alpha \Rightarrow^* \beta }[/math]이고 [math]\displaystyle{ \beta \Rightarrow \gamma }[/math]이면, [math]\displaystyle{ \alpha \Rightarrow^* \gamma }[/math] 입니다.
어떤 문자열 [math]\displaystyle{ w }[/math]가 문법 [math]\displaystyle{ G }[/math]에 포함되는지 확인하려면, 시작 심볼 [math]\displaystyle{ S }[/math]로부터 [math]\displaystyle{ S \Rightarrow^* w }[/math]가 가능한지 보면 됩니다. 파싱(Parsing)은 이러한 유도 과정을 역으로 수행하여, 주어진 터미널 문자열(토큰 스트림)이 시작 심볼로부터 어떻게 유도되었는지를 찾아내는 과정입니다.
- 문장 형식 (Sentential Forms): 문법 [math]\displaystyle{ G=(V, T, S, P) }[/math]에서 시작 심볼 [math]\displaystyle{ S }[/math]로부터 유도될 수 있는 모든 문자열 [math]\displaystyle{ \alpha \in (V \cup T)^* }[/math] (즉, [math]\displaystyle{ S \Rightarrow^* \alpha }[/math]를 만족하는 [math]\displaystyle{ \alpha }[/math])를 문장 형식이라고 합니다. 문장 형식은 터미널과 논터미널을 모두 포함할 수 있습니다.
- 문장 (Sentence): 문장 형식 중에서 논터미널을 전혀 포함하지 않는, 즉 터미널 기호로만 이루어진 문자열을 해당 문법의 문장이라고 합니다.
- 문법의 언어 (Language of a Grammar): 문법 [math]\displaystyle{ G }[/math]가 생성하는 언어 [math]\displaystyle{ L(G) }[/math]는 [math]\displaystyle{ G }[/math]의 모든 문장들의 집합입니다. 즉, [math]\displaystyle{ L(G) = \{ w \in T^* \mid S \Rightarrow^* w \} }[/math] 입니다.
유도 방식: 좌측 최단 유도와 우측 최단 유도
하나의 문장 형식에서 여러 개의 논터미널이 존재할 경우, 어떤 논터미널을 먼저 확장할지에 대한 선택이 필요합니다. 이를 위해 표준적인 유도 방식이 정의되어 있습니다:
- 좌측 최단 유도 (Leftmost Derivation, [math]\displaystyle{ \Rightarrow_l }[/math] 또는 [math]\displaystyle{ \Rightarrow_{lm} }[/math]):
각 유도 단계에서 항상 가장 왼쪽에 있는 논터미널 을 선택하여 생성 규칙을 적용합니다. 만약 [math]\displaystyle{ S \Rightarrow_l^* \alpha }[/math]이면, [math]\displaystyle{ \alpha }[/math]를 좌측 문장 형식(left sentential form) 이라고 합니다.
- 우측 최단 유도 (Rightmost Derivation, [math]\displaystyle{ \Rightarrow_r }[/math] 또는 [math]\displaystyle{ \Rightarrow_{rm} }[/math]):
각 유도 단계에서 항상 가장 오른쪽에 있는 논터미널 을 선택하여 생성 규칙을 적용합니다. 만약 [math]\displaystyle{ S \Rightarrow_r^* \alpha }[/math]이면, [math]\displaystyle{ \alpha }[/math]를 우측 문장 형식(right sentential form) 이라고 합니다. 우측 최단 유도는 특히 LR 파서와 같이 상향식(bottom-up) 파싱에서 유도 과정을 역순으로 구성하는 데 사용됩니다.
어떤 문법에 대해 주어진 문자열이 그 문법에 속한다면, 그 문자열에 대한 좌측 최단 유도와 우측 최단 유도가 각각 존재합니다(때로는 유일하게 존재).
파스 트리 (Parse Tree)
파스 트리(Parse Tree) 또는 구체적인 구문 트리(Concrete Syntax Tree, CST)는 문맥 자유 문법으로부터 특정 문자열이 어떻게 유도되었는지를 시각적으로 보여주는 트리 형태의 표현입니다. 파스 트리는 유도 과정에서 논터미널이 생성 규칙에 의해 대체되는 순서의 변화는 무시하고, 어떤 규칙이 어떤 부분에 적용되었는지만을 나타냅니다. 즉, 동일한 규칙들을 사용하여 동일한 문자열을 유도했다면, 유도 순서(예: 좌측 최단 또는 우측 최단)에 관계없이 동일한 파스 트리가 생성됩니다.
파스 트리는 다음과 같은 속성을 가집니다:
- 루트 노드(Root Node): 문법의 시작 심볼 [math]\displaystyle{ S }[/math]로 레이블링됩니다.
- 내부 노드(Internal Node): 논터미널 기호 [math]\displaystyle{ A \in V }[/math]로 레이블링됩니다.
- 단말 노드(Leaf Node): 터미널 기호 [math]\displaystyle{ a \in T }[/math] 또는 빈 문자열 [math]\displaystyle{ \epsilon }[/math]으로 레이블링됩니다.
- 생성 규칙과의 관계: 만약 어떤 내부 노드가 논터미널 [math]\displaystyle{ A }[/math]로 레이블링되어 있고, 그 자식 노드들이 왼쪽에서 오른쪽으로 [math]\displaystyle{ X_1, X_2, \dots, X_k }[/math]로 레이블링되어 있다면, [math]\displaystyle{ A \rightarrow X_1 X_2 \dots X_k }[/math]는 반드시 문법 [math]\displaystyle{ P }[/math]에 포함된 생성 규칙이어야 합니다. (만약 [math]\displaystyle{ A \rightarrow \epsilon }[/math] 규칙이 적용되었다면, [math]\displaystyle{ A }[/math] 노드는 [math]\displaystyle{ \epsilon }[/math]으로 레이블링된 단일 자식 노드를 가집니다.)
파스 트리의 단말 노드들을 왼쪽에서 오른쪽으로 순서대로 읽으면 원래 유도된 문자열(문장)을 얻을 수 있습니다.
예시: 일반적으로 수식(Expression)을 다루는 문법 예시에서는 다음과 같은 논터미널 기호들이 관례적으로 사용됩니다:
- E: Expression (표현식 또는 수식 전체)
- T: Term (항, 곱셈/나눗셈으로 연결될 수 있는 부분)
- F: Factor (인자, 괄호나 식별자(id) 같은 가장 기본적인 요소)
이러한 관례를 바탕으로 문법 [math]\displaystyle{ E \rightarrow E + E \mid E \star E \mid (E) \mid \text{id} }[/math] 를 생각해 봅시다. 이 문법에 대해 문자열 id + id를 유도하는 한 가지 방법은 [math]\displaystyle{ E \Rightarrow E+E \Rightarrow \text{id}+E \Rightarrow \text{id}+\text{id} }[/math] 입니다. 또 다른 유도 순서로 [math]\displaystyle{ E \Rightarrow E+E \Rightarrow E+\text{id} \Rightarrow \text{id}+\text{id} }[/math]가 있을 수 있습니다. 하지만 이 두 유도 과정은 동일한 파스 트리를 생성합니다.
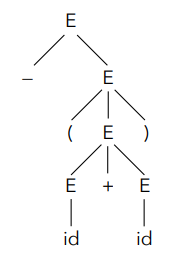
만약 문법이 [math]\displaystyle{ E \rightarrow -E \mid (E) \mid E+E \mid E \star E \mid \text{id} }[/math] 이고 문자열이 -(id+id) 라면, 그 파스 트리는 다음과 같은 구조를 가질 수 있습니다:
- 루트 E는 자식으로
-와 다른 논터미널 E (E1으로 지칭)를 가집니다. - E1은 자식으로
(, 다른 논터미널 E (E2로 지칭),)를 가집니다. - E2는 자식으로 또 다른 논터미널 E (E3로 지칭),
+, 그리고 논터미널 E (E4로 지칭)를 가집니다. - E3과 E4는 각각 자식으로 터미널
id를 가집니다.
모호성 (Ambiguity)
하나의 문법이 특정 문장에 대해 두 개 이상의 서로 다른 파스 트리 를 생성할 수 있다면, 그 문법을 모호한 문법(ambiguous grammar) 이라고 합니다. 모호성은 다음과 같은 경우에도 나타납니다:
- 하나의 문장에 대해 두 개 이상의 서로 다른 좌측 최단 유도가 존재하는 경우.
- 하나의 문장에 대해 두 개 이상의 서로 다른 우측 최단 유도가 존재하는 경우.
프로그래밍 언어에서 모호성은 심각한 문제를 일으킵니다. 왜냐하면 파스 트리는 프로그램의 의미를 결정하는 데 중요한 역할을 하는데, 파스 트리가 여러 개 존재한다는 것은 프로그램의 의미가 여러 가지로 해석될 수 있다는 뜻이기 때문입니다. 예를 들어, 3 + 4 * 5라는 수식은 [math]\displaystyle{ (3+4) \star 5 }[/math]로 해석될 수도 있고, [math]\displaystyle{ 3 + (4 \star 5) }[/math]로 해석될 수도 있습니다. 문법이 모호하면 컴파일러는 어떤 파스 트리를 선택해야 할지 결정할 수 없습니다.
모호성 제거 (Eliminating Ambiguity)
일반적으로 모호한 문법은 모호하지 않은 문법으로 변경하여 사용해야 합니다. 모호성을 제거하는 일반적인 방법은 없지만, 프로그래밍 언어에서 자주 나타나는 모호성(특히 수식 문법에서의 모호성)은 다음과 같은 기법을 사용하여 해결할 수 있습니다:
1. 우선순위(Precedence) 명시: 연산자들 사이에 우선순위를 부여합니다. 예를 들어, 곱셈(*)이 덧셈(+)보다 높은 우선순위를 갖도록 문법을 계층적으로 설계합니다. 1 + 2 * 3은 항상 [math]\displaystyle{ 1 + (2 \star 3) }[/math]으로 해석되도록 합니다.
이를 위해 보통 다음과 같이 여러 레벨의 논터미널을 도입합니다:
[math]\displaystyle{ E \rightarrow E + T \mid T }[/math] (덧셈/뺄셈 레벨, 가장 낮은 우선순위)
[math]\displaystyle{ T \rightarrow T \star F \mid F }[/math] (곱셈/나눗셈 레벨)
[math]\displaystyle{ F \rightarrow (E) \mid \text{id} }[/math] (괄호/기본 요소 레벨, 가장 높은 우선순위)
2. 결합성(Associativity) 명시: 동일한 우선순위를 갖는 연산자들이 연속해서 나타날 때, 왼쪽부터 결합할지(left-associative) 오른쪽부터 결합할지(right-associative)를 문법에 명시합니다. 예를 들어, 덧셈(+)과 곱셈(*)은 보통 왼쪽 결합성을 가집니다. 1 + 2 + 3은 항상 [math]\displaystyle{ (1 + 2) + 3 }[/math]으로 해석되도록 합니다.
- 왼쪽 결합성 은 보통 [math]\displaystyle{ A \rightarrow A \text{ op } B \mid B }[/math] 형태의 좌측 재귀(left-recursive) 생성 규칙으로 표현됩니다 (예: [math]\displaystyle{ E \rightarrow E + T \mid T }[/math]).
- 오른쪽 결합성 은 보통 [math]\displaystyle{ A \rightarrow B \text{ op } A \mid B }[/math] 형태의 우측 재귀(right-recursive) 생성 규칙으로 표현됩니다 (예: 할당 연산자
=는 종종 오른쪽 결합성을 가집니다. [math]\displaystyle{ S \rightarrow \text{id} = S \mid \dots }[/math]).
위의 수정된 문법 [math]\displaystyle{ E \rightarrow E + T \mid T }[/math], [math]\displaystyle{ T \rightarrow T \star F \mid F }[/math], [math]\displaystyle{ F \rightarrow (E) \mid \text{id} }[/math]는 *가 +보다 높은 우선순위를 가지며, 두 연산자 모두 왼쪽 결합성을 갖도록 모호성을 제거한 예입니다.
파서가 처리하기 어려운 문법 변형
파싱 알고리즘(특히 하향식 파서)은 특정 형태의 문법 규칙을 직접 처리하기 어려워하는 경우가 있습니다. 이를 해결하기 위해 문법을 변형하는 기법들이 사용됩니다.
좌측 재귀 제거 (Eliminating Left-Recursion)
생성 규칙이 [math]\displaystyle{ A \rightarrow A\alpha \mid \beta }[/math]와 같이 자기 자신을 가장 왼쪽에서 직접 또는 간접적으로 호출하는 형태를 좌측 재귀(left-recursion) 라고 합니다. (예: [math]\displaystyle{ E \rightarrow E+T }[/math]) 하향식 파서(top-down parser)는 좌측 재귀 규칙을 만나면 무한 루프에 빠질 수 있습니다.
직접적인 좌측 재귀 [math]\displaystyle{ A \rightarrow A\alpha \mid \beta }[/math] (여기서 [math]\displaystyle{ \beta }[/math]는 [math]\displaystyle{ A }[/math]로 시작하지 않음)는 다음과 같은 규칙들로 변형하여 제거할 수 있습니다:
- [math]\displaystyle{ A \rightarrow \beta A' }[/math]
- [math]\displaystyle{ A' \rightarrow \alpha A' \mid \epsilon }[/math]
예를 들어, [math]\displaystyle{ E \rightarrow E+T \mid T }[/math]는 다음과 같이 변형됩니다:
- [math]\displaystyle{ E \rightarrow T E' }[/math]
- [math]\displaystyle{ E' \rightarrow +T E' \mid \epsilon }[/math]
이 변환은 문법이 생성하는 언어를 변경하지 않으면서 좌측 재귀를 우측 재귀 형태로 바꿉니다.
좌측 인수분해 (Left Factoring)
하나의 논터미널에 대해 두 개 이상의 생성 규칙이 동일한 접두사(prefix)로 시작하는 경우 (예: [math]\displaystyle{ S \rightarrow \text{if } E \text{ then } S \text{ else } S }[/math] 와 [math]\displaystyle{ S \rightarrow \text{if } E \text{ then } S }[/math]), 하향식 파서는 어떤 규칙을 선택해야 할지 결정하기 위해 추가적인 입력을 더 읽어야 합니다. 좌측 인수분해(Left Factoring) 는 이러한 공통 접두사를 분리하여 파서가 결정을 쉽게 내릴 수 있도록 문법을 변형하는 기법입니다.
일반적으로 [math]\displaystyle{ A \rightarrow \alpha \beta_1 \mid \alpha \beta_2 }[/math] 형태의 규칙들은 다음과 같이 변형됩니다:
- [math]\displaystyle{ A \rightarrow \alpha A' }[/math]
- [math]\displaystyle{ A' \rightarrow \beta_1 \mid \beta_2 }[/math]
예를 들어, 다음 두 규칙은:
- [math]\displaystyle{ S \rightarrow \text{if } E \text{ then } S \text{ else } S }[/math]
- [math]\displaystyle{ S \rightarrow \text{if } E \text{ then } S }[/math]
다음과 같이 좌측 인수분해 될 수 있습니다:
- [math]\displaystyle{ S \rightarrow \text{if } E \text{ then } S X }[/math]
- [math]\displaystyle{ X \rightarrow \text{else } S \mid \epsilon }[/math]
여기서 [math]\displaystyle{ X }[/math]는 새로운 논터미널입니다.
문맥 자유 문법으로 표현하기 어려운 언어 구조들 (Non-Context-Free Language Constructs)
문맥 자유 문법은 많은 프로그래밍 언어의 구문 구조를 효과적으로 표현할 수 있지만, 모든 언어적 제약을 다룰 수 있는 것은 아닙니다. CFG의 표현력에는 한계가 있으며, 다음과 같은 경우들은 일반적으로 CFG만으로는 검사하기 어렵고, 주로 의미 분석(semantic analysis) 단계에서 처리됩니다.
- 사례 1: 변수 선언 후 사용 확인
언어 [math]\displaystyle{ L_1 = \{ wcw \mid w \in (a|b)^* \} }[/math] 를 생각해봅시다. 이는 [math]\displaystyle{ w }[/math]라는 문자열이 선언되고, 나중에 정확히 동일한 [math]\displaystyle{ w }[/math]가 사용되는 상황을 모델링할 수 있습니다 (예: int x; ... x = 5;). 문맥 자유 문법은 [math]\displaystyle{ w }[/math]의 첫 번째 발생과 두 번째 발생이 동일한 문자열임을 보장하기 어렵습니다. 즉, "식별자는 사용하기 전에 선언되어야 한다"는 규칙은 CFG로 표현하기 힘듭니다.
- 사례 2: 함수 호출 시 인자 개수 일치 확인
언어 [math]\displaystyle{ L_2 = \{ a^n b^m c^n d^m \mid n \ge 1, m \ge 1 \} }[/math] 와 같은 구조는 함수의 정의와 호출에서 인자의 개수나 타입이 일치하는지를 검사하는 상황과 유사합니다. 즉, [math]\displaystyle{ a }[/math]의 개수와 [math]\displaystyle{ c }[/math]의 개수가 같고, [math]\displaystyle{ b }[/math]의 개수와 [math]\displaystyle{ d }[/math]의 개수가 같아야 하는 제약은 CFG로 표현할 수 없습니다.
이러한 속성들은 "문맥에 민감한(context-sensitive)" 정보에 해당하며, 파싱 단계 이후의 의미 분석 단계에서 심볼 테이블(symbol table) 등의 자료구조를 활용하여 검사하는 것이 일반적입니다.
하향식 파싱 (Top-Down Parsing)
문맥 자유 문법(CFG)을 정의했다면, 이제 이 문법을 사용하여 주어진 토큰 스트림으로부터 파스 트리를 구축해야 합니다. 하향식 파싱은 파스 트리의 루트(시작 심볼)에서 시작하여 단말 노드(토큰)에 도달할 때까지 트리를 확장해 나가는 방식입니다.
하향식 파싱의 핵심 문제는 좌측 최단 유도를 수행할 때, 현재 논터미널에 대해 여러 생성 규칙 중 어떤 규칙을 선택해야 하는가입니다. 이 선택을 올바르게 하기 위해 예측(prediction)을 사용하며, 이러한 파싱 방식을 예측 파싱(predictive parsing)이라고도 합니다.
다음은 우리가 자주 사용하는 표현식 문법(Expression Grammar)의 예입니다: [math]\displaystyle{ E \rightarrow T E' }[/math] [math]\displaystyle{ E' \rightarrow + T E' \mid \epsilon }[/math] [math]\displaystyle{ T \rightarrow F T' }[/math] [math]\displaystyle{ T' \rightarrow * F T' \mid \epsilon }[/math] [math]\displaystyle{ F \rightarrow (E) \mid \text{id} }[/math]
파싱 테이블 (Parsing Table)
예측 파서는 파싱 테이블을 사용하여 어떤 생성 규칙을 적용할지 결정합니다. 이 테이블의 행은 논터미널, 열은 터미널 또는 입력의 끝을 나타내는 특수 기호($)입니다. 각 셀에는 적용할 생성 규칙이 들어갑니다.
다음은 위 표현식 문법에 대한 파싱 테이블의 예시입니다:
id |
+ |
* |
( |
) |
$
| |
|---|---|---|---|---|---|---|
| E | [math]\displaystyle{ E \rightarrow T E' }[/math] | [math]\displaystyle{ E \rightarrow T E' }[/math] | ||||
| E' | [math]\displaystyle{ E' \rightarrow + T E' }[/math] | [math]\displaystyle{ E' \rightarrow \epsilon }[/math] | [math]\displaystyle{ E' \rightarrow \epsilon }[/math] | |||
| T | [math]\displaystyle{ T \rightarrow F T' }[/math] | [math]\displaystyle{ T \rightarrow F T' }[/math] | ||||
| T' | [math]\displaystyle{ T' \rightarrow \epsilon }[/math] | [math]\displaystyle{ T' \rightarrow * F T' }[/math] | [math]\displaystyle{ T' \rightarrow \epsilon }[/math] | [math]\displaystyle{ T' \rightarrow \epsilon }[/math] | ||
| F | [math]\displaystyle{ F \rightarrow \text{id} }[/math] | [math]\displaystyle{ F \rightarrow (E) }[/math] |
(표에서 빈 칸은 오류 상황을 나타냅니다.)
예측 파싱 과정 예시
입력 문자열 id + id * id에 대한 예측 파싱 과정은 다음과 같습니다:
| 스택 | 입력 | 적용 규칙 |
|---|---|---|
| [math]\displaystyle{ E$ }[/math] | id + id * id$ |
[math]\displaystyle{ E \rightarrow T E' }[/math] |
| [math]\displaystyle{ T E'$ }[/math] | id + id * id$ |
[math]\displaystyle{ T \rightarrow F T' }[/math] |
| [math]\displaystyle{ F T' E'$ }[/math] | id + id * id$ |
[math]\displaystyle{ F \rightarrow \text{id} }[/math] |
| [math]\displaystyle{ \text{id} T' E'$ }[/math] | id + id * id$ |
match id
|
| [math]\displaystyle{ T' E'$ }[/math] | + id * id$ |
[math]\displaystyle{ T' \rightarrow \epsilon }[/math] |
| [math]\displaystyle{ E'$ }[/math] | + id * id$ |
[math]\displaystyle{ E' \rightarrow + T E' }[/math] |
| [math]\displaystyle{ + T E'$ }[/math] | + id * id$ |
match +
|
| [math]\displaystyle{ T E'$ }[/math] | id * id$ |
[math]\displaystyle{ T \rightarrow F T' }[/math] |
| [math]\displaystyle{ F T' E'$ }[/math] | id * id$ |
[math]\displaystyle{ F \rightarrow \text{id} }[/math] |
| [math]\displaystyle{ \text{id} T' E'$ }[/math] | id * id$ |
match id
|
| [math]\displaystyle{ T' E'$ }[/math] | * id$ |
[math]\displaystyle{ T' \rightarrow * F T' }[/math] |
| [math]\displaystyle{ * F T' E'$ }[/math] | * id$ |
match *
|
| [math]\displaystyle{ F T' E'$ }[/math] | id$ |
[math]\displaystyle{ F \rightarrow \text{id} }[/math] |
| [math]\displaystyle{ \text{id} T' E'$ }[/math] | id$ |
match id
|
| [math]\displaystyle{ T' E'$ }[/math] | $ |
[math]\displaystyle{ T' \rightarrow \epsilon }[/math] |
| [math]\displaystyle{ E'$ }[/math] | $ |
[math]\displaystyle{ E' \rightarrow \epsilon }[/math] |
| [math]\displaystyle{ $ }[/math] | $ |
accept |
예측 파싱 알고리즘
예측 파싱 알고리즘은 스택과 파싱 테이블을 사용합니다.
- 입력: 문자열 [math]\displaystyle{ w }[/math]와 문법 [math]\displaystyle{ G }[/math]에 대한 파싱 테이블 [math]\displaystyle{ M }[/math]
- 출력: [math]\displaystyle{ w }[/math]의 좌측 최단 유도 또는 오류
- 알고리즘:
- 스택의 맨 위를 [math]\displaystyle{ X }[/math], 현재 입력 토큰을 [math]\displaystyle{ a }[/math]라고 합니다.
- [math]\displaystyle{ X }[/math]가 [math]\displaystyle{ $ }[/math] (입력 끝 표시)가 아닐 동안 다음을 반복합니다:
- 만약 [math]\displaystyle{ X = a }[/math]이면, 스택에서 pop하고 다음 입력 토큰을 [math]\displaystyle{ a }[/math]로 설정합니다.
- 그렇지 않고 [math]\displaystyle{ X }[/math]가 터미널이면, 오류를 보고합니다.
- 그렇지 않고 (즉, [math]\displaystyle{ X }[/math]가 논터미널이고) [math]\displaystyle{ M[X, a] }[/math]가 비어있으면, 오류를 보고합니다.
- 그렇지 않고 [math]\displaystyle{ M[X, a] = X \rightarrow Y_1 Y_2 \dots Y_k }[/math] 이면:
- 생성 규칙 [math]\displaystyle{ X \rightarrow Y_1 Y_2 \dots Y_k }[/math]를 출력합니다.
- 스택에서 [math]\displaystyle{ X }[/math]를 pop합니다.
- [math]\displaystyle{ Y_k, Y_{k-1}, \dots, Y_1 }[/math]을 스택에 push합니다 ([math]\displaystyle{ Y_1 }[/math]이 맨 위에 오도록).
- 그렇지 않으면 오류를 보고합니다.
파싱 테이블 구축
파싱 테이블을 구축하려면, 문법의 각 논터미널에 대해 FIRST 집합과 FOLLOW 집합을 계산해야 합니다.
FIRST와 FOLLOW 집합
- FIRST([math]\displaystyle{ \alpha }[/math]): 문자열 [math]\displaystyle{ \alpha }[/math] (터미널과 논터미널의 시퀀스)로부터 유도될 수 있는 문자열들의 시작 부분에 나타날 수 있는 모든 터미널들의 집합입니다.
- 만약 [math]\displaystyle{ \alpha \Rightarrow^* c\beta }[/math] (여기서 [math]\displaystyle{ c }[/math]는 터미널)이면, [math]\displaystyle{ c \in \text{FIRST}(\alpha) }[/math]입니다.
- 만약 [math]\displaystyle{ \alpha \Rightarrow^* \epsilon }[/math]이면, [math]\displaystyle{ \epsilon \in \text{FIRST}(\alpha) }[/math]입니다.
- FOLLOW([math]\displaystyle{ X }[/math]): 논터미널 [math]\displaystyle{ X }[/math]에 대해, 어떤 문장 형식에서 [math]\displaystyle{ X }[/math] 바로 다음에 나타날 수 있는 모든 터미널들의 집합입니다.
- 만약 [math]\displaystyle{ S \Rightarrow^* \alpha X a \beta }[/math] (여기서 [math]\displaystyle{ a }[/math]는 터미널)이면, [math]\displaystyle{ a \in \text{FOLLOW}(X) }[/math]입니다.
- 만약 [math]\displaystyle{ S \Rightarrow^* \alpha X }[/math] (즉, [math]\displaystyle{ X }[/math]가 문장 형식의 끝에 나타남)이면, 입력의 끝을 나타내는 [math]\displaystyle{ $ }[/math] 기호가 [math]\displaystyle{ \text{FOLLOW}(X) }[/math]에 포함됩니다.
표현식 문법 예제에 대한 FIRST 및 FOLLOW 집합 계산: (문법 규칙은 위에서 제시된 번호 1-5를 따릅니다)
- [math]\displaystyle{ \text{FIRST}(F) = \{ '(', \text{id} \} }[/math]
- [math]\displaystyle{ \text{FIRST}(T) = \text{FIRST}(F) = \{ '(', \text{id} \} }[/math]
- [math]\displaystyle{ \text{FIRST}(E) = \text{FIRST}(T) = \{ '(', \text{id} \} }[/math]
- [math]\displaystyle{ \text{FIRST}(E') = \{ '+', \epsilon \} }[/math]
- [math]\displaystyle{ \text{FIRST}(T') = \{ '*', \epsilon \} }[/math]
- [math]\displaystyle{ \text{FOLLOW}(E) = \{ '$', ')' \} }[/math]
- [math]\displaystyle{ \text{FOLLOW}(E') = \text{FOLLOW}(E) = \{ '$', ')' \} }[/math]
- [math]\displaystyle{ \text{FOLLOW}(T) = \text{FIRST}(E') - \{\epsilon\} \cup (\text{if } \epsilon \in \text{FIRST}(E') \text{ then FOLLOW}(E) \text{ else } \emptyset) = \{ '+', '$', ')' \} }[/math]
- [math]\displaystyle{ \text{FOLLOW}(T') = \text{FOLLOW}(T) = \{ '+', '$', ')' \} }[/math]
- [math]\displaystyle{ \text{FOLLOW}(F) = \text{FIRST}(T') - \{\epsilon\} \cup (\text{if } \epsilon \in \text{FIRST}(T') \text{ then FOLLOW}(T) \text{ else } \emptyset) = \{ '*', '+', '$', ')' \} }[/math]
FIRST 집합 계산 알고리즘
모든 문법 기호 [math]\displaystyle{ X }[/math]에 대해 [math]\displaystyle{ \text{FIRST}(X) }[/math]를 계산하려면, 더 이상 터미널이나 [math]\displaystyle{ \epsilon }[/math]이 어떤 FIRST 집합에도 추가될 수 없을 때까지 다음 규칙들을 적용합니다:
- [math]\displaystyle{ X }[/math]가 터미널이면, [math]\displaystyle{ \text{FIRST}(X) = \{X\} }[/math]입니다.
- [math]\displaystyle{ X }[/math]가 논터미널이고 [math]\displaystyle{ X \rightarrow Y_1 Y_2 \dots Y_k }[/math] ([math]\displaystyle{ k \ge 1 }[/math])가 생성 규칙일 때:
- 어떤 [math]\displaystyle{ i }[/math]에 대해 [math]\displaystyle{ a \in \text{FIRST}(Y_i) }[/math]이고 [math]\displaystyle{ \epsilon }[/math]이 모든 [math]\displaystyle{ \text{FIRST}(Y_1), \dots, \text{FIRST}(Y_{i-1}) }[/math]에 있다면 (여기서 [math]\displaystyle{ a }[/math]는 터미널), [math]\displaystyle{ a }[/math]를 [math]\displaystyle{ \text{FIRST}(X) }[/math]에 추가합니다.
- 모든 [math]\displaystyle{ j=1, \dots, k }[/math]에 대해 [math]\displaystyle{ \epsilon \in \text{FIRST}(Y_j) }[/math]이면, [math]\displaystyle{ \epsilon }[/math]을 [math]\displaystyle{ \text{FIRST}(X) }[/math]에 추가합니다.
- [math]\displaystyle{ X \rightarrow \epsilon }[/math]이 생성 규칙이면, [math]\displaystyle{ \epsilon }[/math]을 [math]\displaystyle{ \text{FIRST}(X) }[/math]에 추가합니다.
문자열 [math]\displaystyle{ X_1 X_2 \dots X_n }[/math]에 대한 FIRST 집합은 다음과 같이 계산합니다:
- [math]\displaystyle{ \text{FIRST}(X_1) }[/math]의 모든 non-[math]\displaystyle{ \epsilon }[/math] 심볼들을 추가합니다.
- [math]\displaystyle{ \epsilon \in \text{FIRST}(X_1) }[/math]이면, [math]\displaystyle{ \text{FIRST}(X_2) }[/math]의 모든 non-[math]\displaystyle{ \epsilon }[/math] 심볼들을 추가합니다.
- [math]\displaystyle{ \epsilon \in \text{FIRST}(X_1) }[/math]이고 [math]\displaystyle{ \epsilon \in \text{FIRST}(X_2) }[/math]이면, [math]\displaystyle{ \text{FIRST}(X_3) }[/math]의 모든 non-[math]\displaystyle{ \epsilon }[/math] 심볼들을 추가합니다.
- ... 이런 식으로 계속 진행합니다.
- 모든 [math]\displaystyle{ i }[/math]에 대해 [math]\displaystyle{ \epsilon \in \text{FIRST}(X_i) }[/math]이면, [math]\displaystyle{ \epsilon }[/math]을 추가합니다.
FOLLOW 집합 계산 알고리즘
모든 논터미널 [math]\displaystyle{ A }[/math]에 대해 [math]\displaystyle{ \text{FOLLOW}(A) }[/math]를 계산하려면, 어떤 FOLLOW 집합에도 더 이상 아무것도 추가될 수 없을 때까지 다음 규칙들을 적용합니다:
- 문법의 시작 심볼 [math]\displaystyle{ S }[/math]에 대해, [math]\displaystyle{ $ }[/math]를 [math]\displaystyle{ \text{FOLLOW}(S) }[/math]에 추가합니다.
- 생성 규칙 [math]\displaystyle{ A \rightarrow \alpha B \beta }[/math]가 있다면, [math]\displaystyle{ \text{FIRST}(\beta) }[/math]에 있는 모든 것( [math]\displaystyle{ \epsilon }[/math] 제외)을 [math]\displaystyle{ \text{FOLLOW}(B) }[/math]에 추가합니다.
- 생성 규칙 [math]\displaystyle{ A \rightarrow \alpha B }[/math]가 있거나, 또는 [math]\displaystyle{ A \rightarrow \alpha B \beta }[/math]에서 [math]\displaystyle{ \text{FIRST}(\beta) }[/math]가 [math]\displaystyle{ \epsilon }[/math]을 포함한다면, [math]\displaystyle{ \text{FOLLOW}(A) }[/math]에 있는 모든 것을 [math]\displaystyle{ \text{FOLLOW}(B) }[/math]에 추가합니다.
파싱 테이블 M[A, a] 구축 알고리즘
- 입력: 문법 [math]\displaystyle{ G }[/math]
- 출력: 파싱 테이블 [math]\displaystyle{ M }[/math]
- 알고리즘: 문법의 각 생성 규칙 [math]\displaystyle{ A \rightarrow \alpha }[/math]에 대해 다음을 수행합니다:
- [math]\displaystyle{ \text{FIRST}(\alpha) }[/math]에 있는 각 터미널 [math]\displaystyle{ a }[/math]에 대해, [math]\displaystyle{ M[A, a] }[/math]에 [math]\displaystyle{ A \rightarrow \alpha }[/math]를 추가합니다.
- 만약 [math]\displaystyle{ \epsilon \in \text{FIRST}(\alpha) }[/math]이면, [math]\displaystyle{ \text{FOLLOW}(A) }[/math]에 있는 각 터미널 [math]\displaystyle{ b }[/math] (또는 [math]\displaystyle{ $ }[/math])에 대해, [math]\displaystyle{ M[A, b] }[/math] (또는 [math]\displaystyle{ M[A, $] }[/math])에 [math]\displaystyle{ A \rightarrow \alpha }[/math]를 추가합니다.
- 만약 [math]\displaystyle{ \text{FIRST}(\alpha) \cap \text{FIRST}(\beta) \neq \emptyset }[/math] 인 두 규칙 [math]\displaystyle{ A \rightarrow \alpha }[/math] 와 [math]\displaystyle{ A \rightarrow \beta }[/math] 가 있다면, 문법은 예측 파싱으로 파싱될 수 없습니다.
- 이러한 예측 파싱으로 파싱 가능한 문법을 LL(1) 문법이라고 합니다 (Left-to-right scan, Leftmost derivation, 1-symbol lookahead).
상향식 파싱 (Bottom-Up Parsing)
지금까지 파스 트리의 루트(시작 심볼)에서부터 시작하여 단말 노드로 내려가면서 트리를 구축하는 하향식 파싱 방법에 대해 알아보았습니다. 이제는 정반대의 접근 방식인 상향식 파싱(Bottom-Up Parsing)에 대해 자세히 살펴봅시다.
상향식 파싱은 입력 문자열(즉, 파스 트리의 단말 노드들)에서 시작하여, 이들을 점차적으로 문법 규칙에 따라 결합하고 상위의 논터미널로 대체(축약, reduce)해 나갑니다. 이 과정을 반복하여 최종적으로 트리의 루트 노드인 시작 심볼에 도달하는 방식으로 파스 트리를 구축합니다. 이 과정은 마치 오른쪽 최단 유도(Rightmost Derivation)를 역순으로 만들어가는 것과 같습니다. 예를 들어, id*id라는 입력이 주어졌을 때, 상향식 파서는 [math]\displaystyle{ \text{id}*\text{id} \Rightarrow F*\text{id} \Rightarrow T*\text{id} \Rightarrow T*F \Rightarrow T \Rightarrow E }[/math] 와 같이 오른쪽 최단 유도의 역순으로 진행됩니다.
상향식 파싱은 일반적으로 하향식 파싱보다 더 넓은 범위의 문법을 처리할 수 있어 강력한 파싱 전략으로 알려져 있습니다.
핸들 (Handle)
상향식 파싱의 핵심 과정은 현재까지 스캔한 입력 문자열의 어느 부분을 어떤 문법 규칙을 사용해 논터미널로 축약(reduce)할 것인지 결정하는 것입니다. 이때, 축약의 대상이 되는 부분 문자열을 핸들(Handle)이라고 부릅니다. 보다 정확하게, 핸들은 다음 두 가지 조건을 만족합니다:
- 현재 처리 중인 오른쪽 문장 형식(right sentential form) 내의 특정 부분 문자열이어야 하며, 이 부분 문자열은 어떤 생성 규칙 [math]\displaystyle{ A \rightarrow \beta }[/math]의 우변 [math]\displaystyle{ \beta }[/math]와 정확히 일치해야 합니다.
- 이 부분 문자열 [math]\displaystyle{ \beta }[/math]를 해당 규칙의 좌변인 논터미널 [math]\displaystyle{ A }[/math]로 치환(축약)했을 때, 그 결과가 여전히 오른쪽 최단 유도의 한 단계 이전 형태가 되어야 합니다. 즉, 시작 심볼로부터 원래의 오른쪽 문장 형식으로 도달하는 오른쪽 최단 유도 과정 중에 나타나는 유효한 단계여야 합니다.
상향식 파서의 기본 작업은 "핸들을 찾고, 그 핸들을 해당하는 논터미널로 축약하는" 과정을 반복하는 것입니다. 예를 들어, 문장 형식 [math]\displaystyle{ T*id }[/math] 에서 id는 [math]\displaystyle{ F \rightarrow \text{id} }[/math] 규칙의 핸들이 될 수 있습니다. 이를 [math]\displaystyle{ F }[/math]로 축약하면 [math]\displaystyle{ T*F }[/math]가 됩니다.
LR 파싱
LR 파싱은 가장 대표적이고 강력한 상향식 파싱 기법 중 하나입니다. LR이라는 이름은 다음을 의미합니다:
- L: 입력 문자열을 Left-to-right (왼쪽에서 오른쪽으로) 스캔합니다.
- R: 오른쪽 최단 유도(Rightmost derivation)를 역순으로 구성합니다.
- (k): 다음 입력 토큰을 최대 k개까지 미리 보고(lookahead) 파싱 결정을 내립니다. (실제로는 k=1인 LR(1) 파서가 가장 일반적으로 사용되며, 여기서 k는 보통 생략되거나 1로 간주됩니다.)
LR 파서는 결정적 유한 오토마타(DFA)를 사용하여 언제 쉬프트(shift)하고 언제 축약(reduce)할지, 특히 핸들을 어떻게 인식할지를 결정합니다.
LR 파싱 개요
LR 파서는 주로 다음과 같은 구성요소로 이루어집니다:
- 입력 버퍼: 아직 처리되지 않은 나머지 토큰 스트림을 저장합니다. 입력의 끝은 특수 기호 [math]\displaystyle{ $ }[/math]로 표시됩니다.
- 스택: 파싱 과정에서 상태(state)들을 저장합니다. 각 상태는 지금까지 처리한 입력 부분에 대한 정보를 요약합니다.
- 파싱 테이블: 현재 스택의 최상단 상태와 다음 입력 토큰(lookahead)을 기반으로 파서가 수행할 행동(action)과 다음 상태(goto)를 결정하는 데 사용됩니다.
파서는 현재 스택의 최상단 상태와 미리 본 입력 토큰을 참조하여 파싱 테이블에서 다음 행동을 결정합니다. 주요 행동은 다음과 같습니다:
- 쉬프트 (Shift s): 현재 입력 토큰을 스택으로 옮기고, 파서는 상태 [math]\displaystyle{ s }[/math]로 전이합니다. 입력 포인터는 다음 토큰으로 이동합니다.
- 축약 (Reduce [math]\displaystyle{ A \rightarrow \beta }[/math]): 스택의 최상단에 핸들 [math]\displaystyle{ \beta }[/math]가 인식되었음을 의미합니다. 스택에서 [math]\displaystyle{ \beta }[/math]에 해당하는 심볼 수만큼 (정확히는 [math]\displaystyle{ 2 \times |\beta| }[/math] 개의 상태와 심볼, 또는 상태만을 관리한다면 [math]\displaystyle{ |\beta| }[/math] 개의 상태) pop 합니다. 그 후, 스택의 새로운 최상단 상태와 규칙의 좌변인 논터미널 [math]\displaystyle{ A }[/math]를 사용하여 GOTO 테이블을 참조, 다음 상태를 결정하여 [math]\displaystyle{ A }[/math]와 함께 그 상태를 스택에 push 합니다.
- 수락 (Accept): 입력 문자열 전체가 성공적으로 파싱되어 시작 심볼로 축약되었음을 의미합니다. 파싱이 성공적으로 종료됩니다.
- 오류 (Error): 파싱 테이블에 유효한 행동이 없는 경우 구문 오류가 발생했음을 의미합니다.
LR 파싱 테이블과 핸들 인식
LR 파싱 테이블은 DFA(LR 오토마톤)로부터 생성됩니다. 이 DFA의 각 상태는 현재까지 가능한 파싱 상태를 나타내며, 주로 "LR 아이템"이라는 특별한 생성 규칙 형태로 표현됩니다.
테이블은 두 부분으로 구성됩니다:
- ACTION[상태, 터미널]: 현재 스택 top의 '상태'와 다음 입력 '터미널'에 따라 수행할 동작 (shift, reduce, accept, error)을 지정합니다.
- GOTO[상태, 논터미널]: reduce 동작 후, 스택 top의 '상태'와 방금 축약되어 생성된 '논터미널'에 따라 전이할 다음 상태를 지정합니다.
예를 들어, 아래는 표현식 문법에 대한 LR 파싱 테이블의 일부입니다 (s는 shift, r은 reduce, 숫자는 상태 또는 규칙 번호, acc는 accept, g는 goto).
| 상태 | id | + | * | ( | ) | $ | E | T | F |
|---|---|---|---|---|---|---|---|---|---|
| 0 | s5 | s4 | g1 | g2 | g3 | ||||
| 1 | s6 | acc | |||||||
| 2 | r2([math]\displaystyle{ E \rightarrow T }[/math]) | s7 | r2([math]\displaystyle{ E \rightarrow T }[/math]) | r2([math]\displaystyle{ E \rightarrow T }[/math]) | |||||
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
만약 현재 상태가 2이고 다음 입력이 +이면, 테이블은 [math]\displaystyle{ E \rightarrow T }[/math] 규칙(규칙 2번)으로 축약(r2)하라고 지시합니다. 만약 다음 입력이 *이면, s7 (7번 상태로 쉬프트)을 지시합니다.
LR 파싱 과정 (스택에 상태 저장)
실제 LR 파서는 스택에 (상태, 심볼) 쌍 대신 주로 상태 번호만을 저장하여 효율성을 높입니다. 심볼은 암묵적으로 각 상태와 연관됩니다.
다음은 id * id$ 입력에 대한 LR 파싱 과정의 예시입니다 (위 테이블 및 표현식 문법 기준).
| 스택 (상태) | (암묵적) 심볼 스택 | 입력 | 행동 |
|---|---|---|---|
0 |
$ |
id * id$ |
ACTION[0,id]=s5 (shift 5) |
0 5 |
$id |
* id$ |
ACTION[5,*]=r6 ([math]\displaystyle{ F \rightarrow \text{id} }[/math]), GOTO[0,F]=g3 |
0 3 |
$F |
* id$ |
ACTION[3,*]=r4 ([math]\displaystyle{ T \rightarrow F }[/math]), GOTO[0,T]=g2 |
0 2 |
$T |
* id$ |
ACTION[2,*]=s7 (shift 7) |
0 2 7 |
$T* |
id$ |
ACTION[7,id]=s5 (shift 5) |
0 2 7 5 |
$T*id |
$ |
ACTION[5,$]=r6 ([math]\displaystyle{ F \rightarrow \text{id} }[/math]), GOTO[7,F]=g10 |
0 2 7 10 |
$T*F |
$ |
ACTION[10,$]=r3 ([math]\displaystyle{ T \rightarrow T*F }[/math]), GOTO[0,T]=g2 |
0 2 |
$T |
$ |
ACTION[2,$]=r2 ([math]\displaystyle{ E \rightarrow T }[/math]), GOTO[0,E]=g1 |
0 1 |
$E |
$ |
ACTION[1,$]=acc (accept) |
LR 파서의 종류 및 생성
LR 파서는 얼마나 많은 lookahead 토큰을 사용하는지와 파싱 테이블을 구축하는 방식에 따라 LR(0), SLR(1), LALR(1), LR(1) 등으로 나뉩니다.
LR(0) 아이템과 LR(0) 오토마톤
- LR(0) 아이템: 생성 규칙의 우변에 점(dot, [math]\displaystyle{ \cdot }[/math])을 추가하여 파싱 진행 상태를 나타냅니다. 예를 들어, [math]\displaystyle{ A \rightarrow \cdot XYZ, A \rightarrow X \cdot YZ, A \rightarrow XY \cdot Z, A \rightarrow XYZ \cdot }[/math] 와 같습니다.
- CLOSURE 연산: 아이템 집합 [math]\displaystyle{ I }[/math]에 대해, [math]\displaystyle{ I }[/math]의 모든 아이템과, [math]\displaystyle{ A \rightarrow \alpha \cdot B \beta }[/math] 형태의 아이템이 있을 때 모든 [math]\displaystyle{ B \rightarrow \cdot \gamma }[/math] 규칙을 추가하여 아이템 집합을 확장합니다. 이 과정을 더 이상 아이템이 추가되지 않을 때까지 반복합니다.
- GOTO(I, X) 연산: 아이템 집합 [math]\displaystyle{ I }[/math]와 문법 기호 [math]\displaystyle{ X }[/math]에 대해, [math]\displaystyle{ I }[/math] 내의 [math]\displaystyle{ A \rightarrow \alpha \cdot X \beta }[/math] 아이템들에서 점을 [math]\displaystyle{ X }[/math] 다음으로 옮긴 [math]\displaystyle{ A \rightarrow \alpha X \cdot \beta }[/math] 형태의 아이템들의 집합에 CLOSURE를 적용하여 새로운 상태(아이템 집합)를 만듭니다.
- LR(0) 오토마톤: 문법을 확장한 규칙 [math]\displaystyle{ S' \rightarrow S }[/math]의 아이템 [math]\displaystyle{ S' \rightarrow \cdot S }[/math]에 CLOSURE를 적용한 것을 초기 상태로 하여, GOTO 연산을 통해 모든 가능한 상태와 전이를 찾아 DFA를 구성합니다.
LR(0) 및 SLR 파싱 테이블 구축
- LR(0) 테이블:
* GOTO(I, a) = J (a는 터미널)이면, ACTION[I, a] = shift J. * GOTO(I, A) = J (A는 논터미널)이면, GOTO[I, A] = J. * [math]\displaystyle{ S' \rightarrow S \cdot }[/math] 이 [math]\displaystyle{ I }[/math]에 있으면, ACTION[I, $] = accept. * [math]\displaystyle{ A \rightarrow \alpha \cdot }[/math] (단, [math]\displaystyle{ A \neq S' }[/math])가 [math]\displaystyle{ I }[/math]에 있으면, 모든 터미널 [math]\displaystyle{ t }[/math] 및 [math]\displaystyle{ $ }[/math]에 대해 ACTION[I, t] = reduce [math]\displaystyle{ A \rightarrow \alpha }[/math]. 이 마지막 조건 때문에 LR(0)는 충돌이 발생하기 쉽습니다.
- SLR(Simple LR) 테이블: LR(0)의 reduce 행동을 개선합니다. [math]\displaystyle{ A \rightarrow \alpha \cdot }[/math] 이 [math]\displaystyle{ I }[/math]에 있을 때, [math]\displaystyle{ \text{FOLLOW}(A) }[/math]에 속하는 각 터미널 [math]\displaystyle{ t }[/math]에 대해서만 ACTION[I, t] = reduce [math]\displaystyle{ A \rightarrow \alpha }[/math]를 추가합니다. 이를 통해 많은 불필요한 충돌을 줄일 수 있습니다.
파싱 테이블 충돌 (Conflicts)
파싱 테이블의 한 셀에 두 가지 이상의 행동이 정의되면 충돌이 발생합니다.
- 쉬프트/리듀스 충돌 (Shift/Reduce Conflict): 동일한 상태와 입력 토큰에 대해 쉬프트와 리듀스 행동 중 하나를 선택해야 하는 경우.
- 리듀스/리듀스 충돌 (Reduce/Reduce Conflict): 동일한 상태와 입력 토큰에 대해 두 가지 이상의 다른 생성 규칙으로 리듀스할 수 있는 경우.
충돌이 없는 LR(0) 문법이나 SLR 문법은 해당 파싱 방법으로 파싱이 가능합니다. 하지만 SLR로도 해결되지 않는 충돌이 존재합니다.
LALR(1) 및 LR(1) 파서
더 강력한 LR 파싱 방법으로 LR(1)과 LALR(1)이 있습니다.
- LR(1) 파서: LR(0) 아이템에 추가적으로 하나의 lookahead 터미널을 포함하는 LR(1) 아이템 ([math]\displaystyle{ (A \rightarrow \alpha \cdot \beta, a) }[/math])을 사용합니다. 이는 축약 결정을 내릴 때 lookahead 정보를 활용하여 매우 강력한 파싱 능력을 제공하지만, 생성되는 상태의 수가 매우 많아질 수 있다는 단점이 있습니다.
- LALR(1) (Look-Ahead LR) 파서: LR(1) 오토마톤의 상태들 중 핵심 LR(0) 아이템 부분은 같지만 lookahead만 다른 상태들을 병합하여 상태 수를 줄인 방식입니다. LR(1)보다는 약간 약하지만 SLR보다는 훨씬 강력하며, 파싱 테이블의 크기가 LR(0) 오토마톤과 동일하여 실용적으로 널리 사용됩니다 (예: Yacc, Bison).
상향식 파싱은 이처럼 다양한 기법과 정교한 테이블 구축 과정을 통해 강력한 파싱 능력을 제공하며, 많은 프로그래밍 언어 컴파일러에서 채택하고 있는 방식입니다.