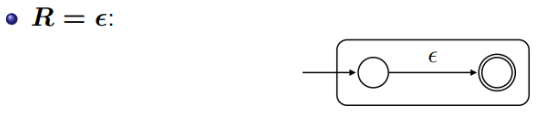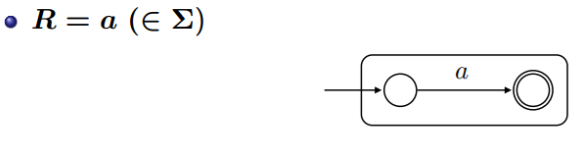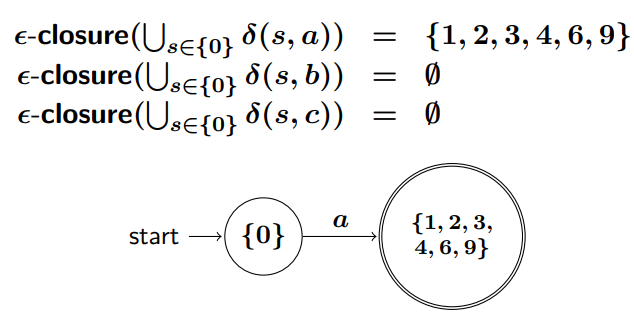어휘 분석

Lecture 2에서는 컴파일러의 첫 번째 단계인 어휘 분석(Lexical Analysis)에 대해 다룹니다. 어휘 분석은 소스 프로그램을 문자(character)의 스트림으로 받아, 이를 문법적으로 의미 있는 최소 단위인 토큰(token)의 스트림으로 변환하는 과정입니다. 어휘 분석기는 흔히 렉서(lexer) 또는 스캐너(scanner) 라고도 불립니다.

어휘 분석기의 역할

어휘 분석기는 미리 정의된 패턴(pattern) 들을 사용하여 입력 문자열에서 토큰을 식별합니다. 예를 들어, 프로그래밍 언어에서 식별자(identifier), 키워드(keyword), 숫자(number), 연산자(operator) 등은 각각 고유한 패턴을 가집니다. 어휘 분석기는 이러한 패턴을 인식하고, 공백(whitespace), 탭, 줄 바꿈 문자나 구두점(punctuation), 또는 다른 토큰의 시작과 같은 구분자(delimiter)를 기준으로 문자열을 분리하여 토큰을 추출합니다.

예를 들어, 아래와 같은 C 언어 코드가 주어졌다고 가정해 봅시다.

float match0 (char *s) /* find a zero */
{
    if (!strncmp(s, "0.0", 3))
        return 0.0;
}

어휘 분석기는 이 코드를 다음과 같은 토큰의 연속으로 변환합니다:

여기서 ID(match0)는 match0이라는 값을 가진 식별자(Identifier) 타입의 토큰을, NUM(3)은 값 3을 가진 숫자(Number) 타입의 토큰을 나타냅니다. EOF는 파일의 끝(End Of File)을 나타내는 특수한 토큰입니다.

어휘 분석 과정을 이해하고 구현하기 위해서는 다음 세 가지 핵심 요소를 알아야 합니다:

명세 (Specification): 토큰과 같은 어휘적 패턴을 어떻게 정확하게 정의하고 명시할 것인가? (이를 위해 주로 정규 표현식(Regular Expression) 이 사용됩니다.)
인식 (Recognition): 명시된 어휘 패턴을 입력 문자열에서 어떻게 효율적으로 인식할 것인가? (이를 위해 주로 결정적 유한 오토마타(Deterministic Finite Automaton, DFA) 가 사용됩니다.)
자동화 (Automation): 주어진 명세(정규 표현식)로부터 패턴 인식기(DFA)를 어떻게 자동으로 생성할 것인가? (이를 위해 톰슨 구성법(Thompson's construction) 으로 정규 표현식에서 NFA를 만들고, 부분집합 구성법(subset construction) 으로 NFA에서 DFA를 만듭니다.)

명세 (Specification): 어휘 패턴의 정의

어휘 분석의 가장 기본적인 출발점은 토큰으로 인식될 문자열 패턴을 정의하는 것입니다. 이를 위해 형식 언어 이론의 개념들이 사용됩니다.

알파벳 (Alphabet)

알파벳(alphabet) [math]\displaystyle{ \Sigma }[/math]는 문자(character) 또는 기호(symbol)들의 유한하고 비어있지 않은 집합(finite, non-empty set)을 의미합니다. 예를 들어, C 언어의 알파벳은 ASCII 문자 집합이 될 수 있고, 이진수를 다룬다면 알파벳은 [math]\displaystyle{ \{ 0, 1\} }[/math]이 됩니다.

문자열 (Strings)

문자열(string)은 특정 알파벳 [math]\displaystyle{ \Sigma }[/math]에 속한 기호들을 유한하게 나열한 순서(finite sequence)입니다.

길이가 0인 문자열, 즉 아무 기호도 포함하지 않는 문자열을 빈 문자열(empty string) 이라고 하며, 보통 [math]\displaystyle{ \epsilon }[/math] (입실론)으로 표기합니다.
두 문자열 [math]\displaystyle{ w }[/math]와 [math]\displaystyle{ v }[/math]를 이어 붙이는 것을 연결(concatenation) 이라고 하며 [math]\displaystyle{ wv }[/math]로 나타냅니다.
문자열 [math]\displaystyle{ w }[/math]의 기호 순서를 거꾸로 뒤집은 것을 [math]\displaystyle{ w }[/math]의 역순(reverse) 이라 하고 [math]\displaystyle{ w^R }[/math]로 씁니다.
문자열 [math]\displaystyle{ w }[/math]에 포함된 기호의 개수를 [math]\displaystyle{ w }[/math]의 길이(length) 라고 하며 [math]\displaystyle{ |w| }[/math]로 표기합니다. 빈 문자열의 길이는 [math]\displaystyle{ |\epsilon|=0 }[/math]이며, 어떤 문자열 [math]\displaystyle{ v }[/math]에 기호 하나 [math]\displaystyle{ a }[/math]를 연결한 [math]\displaystyle{ va }[/math]의 길이는 [math]\displaystyle{ |v|+1 }[/math]입니다 (여기서 [math]\displaystyle{ a }[/math]는 단일 기호).
문자열 [math]\displaystyle{ w }[/math]가 [math]\displaystyle{ vu }[/math]의 형태로 표현될 때, [math]\displaystyle{ v }[/math]를 [math]\displaystyle{ w }[/math]의 접두사(prefix), [math]\displaystyle{ u }[/math]를 [math]\displaystyle{ w }[/math]의 접미사(suffix) 라고 합니다.
[math]\displaystyle{ \Sigma^k }[/math]는 알파벳 [math]\displaystyle{ \Sigma }[/math]에 속한 기호들로 만들 수 있는 길이가 정확히 [math]\displaystyle{ k }[/math]인 모든 문자열의 집합을 나타냅니다.
[math]\displaystyle{ \Sigma^\star }[/math]는 알파벳 [math]\displaystyle{ \Sigma }[/math]로 만들 수 있는 모든 길이의 문자열 집합을 의미하며, 빈 문자열 [math]\displaystyle{ \epsilon }[/math]을 포함합니다 ([math]\displaystyle{ \Sigma^\star = \Sigma^0 \cup \Sigma^1 \cup \Sigma^2 \cup \dots = \bigcup_{i \in \mathbb{N}} \Sigma^i }[/math]).
[math]\displaystyle{ \Sigma^+ }[/math]는 [math]\displaystyle{ \Sigma^\star }[/math]에서 빈 문자열 [math]\displaystyle{ \epsilon }[/math]을 제외한, 즉 길이가 1 이상인 모든 문자열의 집합입니다 ([math]\displaystyle{ \Sigma^+ = \Sigma^1 \cup \Sigma^2 \cup \dots = \Sigma^\star \setminus \{\epsilon\} }[/math]).

언어 (Languages)

형식 언어 이론에서 언어(language) [math]\displaystyle{ L }[/math]은 특정 알파벳 [math]\displaystyle{ \Sigma }[/math]로부터 생성될 수 있는 모든 문자열의 집합인 [math]\displaystyle{ \Sigma^\star }[/math]의 부분집합([math]\displaystyle{ L \subseteq \Sigma^\star }[/math])으로 정의됩니다. 즉, 어떤 규칙이나 조건을 만족하는 문자열들의 모임입니다.

언어들 사이에는 다음과 같은 연산들이 정의될 수 있습니다:

합집합 (Union): [math]\displaystyle{ L_1 \cup L_2 = \{ w \mid w \in L_1 \text{ or } w \in L_2\} }[/math]
교집합 (Intersection): [math]\displaystyle{ L_1 \cap L_2 = \{ w \mid w \in L_1 \text{ and } w \in L_2\} }[/math]
차집합 (Difference): [math]\displaystyle{ L_1 - L_2 = \{ w \mid w \in L_1 \text{ and } w \notin L_2\} }[/math]
역순 (Reverse): [math]\displaystyle{ L^R = \{ w^R \mid w \in L\} }[/math]
여집합 (Complement): [math]\displaystyle{ \overline{L} = \Sigma^\star - L }[/math]
연결 (Concatenation): [math]\displaystyle{ L_1 L_2 = \{ xy \mid x \in L_1 \text{ and } y \in L_2\} }[/math] (언어 [math]\displaystyle{ L_1 }[/math]의 문자열과 언어 [math]\displaystyle{ L_2 }[/math]의 문자열을 순서대로 연결하여 만들 수 있는 모든 문자열의 집합)
거듭제곱 (Power): [math]\displaystyle{ L^n }[/math]은 언어 [math]\displaystyle{ L }[/math]을 [math]\displaystyle{ n }[/math]번 연결한 것입니다.

 * [math]\displaystyle{ L^0 = \{\epsilon\} }[/math] (정의에 따라 빈 문자열만을 원소로 가짐)
 * [math]\displaystyle{ L^n = L L^{n-1} }[/math] (또는 [math]\displaystyle{ L^{n-1}L }[/math]) ([math]\displaystyle{ n \ge 1 }[/math])

스타 클로저 (Star-closure 또는 Kleene closure): [math]\displaystyle{ L^\star }[/math]는 언어 [math]\displaystyle{ L }[/math]의 문자열들을 0번 이상 연결하여 만들 수 있는 모든 문자열의 집합입니다. 즉, [math]\displaystyle{ L^\star = L^0 \cup L^1 \cup L^2 \cup \dots = \bigcup_{i \ge 0} L^i }[/math].
양성 클로저 (Positive closure): [math]\displaystyle{ L^+ }[/math]는 언어 [math]\displaystyle{ L }[/math]의 문자열들을 1번 이상 연결하여 만들 수 있는 모든 문자열의 집합입니다. 즉, [math]\displaystyle{ L^+ = L^1 \cup L^2 \cup L^3 \cup \dots = \bigcup_{i \ge 1} L^i }[/math]. 이는 [math]\displaystyle{ L^\star = L^+ \cup \{ \epsilon\} }[/math] (단, [math]\displaystyle{ L }[/math]이 [math]\displaystyle{ \epsilon }[/math]을 포함하지 않을 경우) 또는 [math]\displaystyle{ L^+ = L L^\star }[/math] 관계를 가집니다.

정규 표현식 (Regular Expressions)

정규 표현식(Regular Expression, RE)은 특정 규칙을 가진 문자열의 집합, 즉 정규 언어(Regular Language) 를 간결하게 명시하기 위해 사용되는 메타 언어(meta-language) 입니다. 어휘 분석에서는 다양한 토큰의 패턴(예: 식별자, 숫자, 특정 키워드)을 정의하는 데 주로 활용됩니다. 정규 표현식 자체도 하나의 언어이므로, 고유한 구문(syntax)과 의미(semantics)를 가집니다.

정규 표현식의 구문 (Syntax)

정규 표현식 [math]\displaystyle{ R }[/math]은 더 단순한 정규 표현식들을 조합하여 재귀적으로 정의됩니다. 일반적인 정규 표현식의 구문은 다음과 같은 규칙으로 정의될 수 있습니다 (여기서 [math]\displaystyle{ R, R_1, R_2 }[/math]는 정규 표현식을 나타냅니다):

기본 심볼 (Base Symbols):
- [math]\displaystyle{ \emptyset }[/math]: 빈 집합(empty set)을 나타내는 정규 표현식. 어떤 문자열도 포함하지 않는 언어를 의미합니다.
- [math]\displaystyle{ \epsilon }[/math]: 빈 문자열(empty string) [math]\displaystyle{ \epsilon }[/math]만을 포함하는 언어를 나타내는 정규 표현식입니다.
- [math]\displaystyle{ a }[/math]: 알파벳 [math]\displaystyle{ \Sigma }[/math]에 속하는 임의의 단일 기호 [math]\displaystyle{ a }[/math]에 대해, [math]\displaystyle{ a }[/math]는 문자열 [math]\displaystyle{ a }[/math]만을 포함하는 언어를 나타내는 정규 표현식입니다.
연산 (Operations):
- [math]\displaystyle{ R_1 | R_2 }[/math] (선택, Alternation): [math]\displaystyle{ R_1 }[/math]이 나타내는 언어와 [math]\displaystyle{ R_2 }[/math]가 나타내는 언어의 합집합 을 의미합니다. 즉, [math]\displaystyle{ R_1 }[/math]에 속하거나 [math]\displaystyle{ R_2 }[/math]에 속하는 문자열들을 나타냅니다. (때로는 [math]\displaystyle{ R_1 + R_2 }[/math]로 표기하기도 합니다.)
- [math]\displaystyle{ R_1 R_2 }[/math] (연결, Concatenation): [math]\displaystyle{ R_1 }[/math]이 나타내는 언어의 문자열 뒤에 [math]\displaystyle{ R_2 }[/math]가 나타내는 언어의 문자열을 이어 붙여 만들어지는 모든 문자열의 집합을 의미합니다. (때로는 [math]\displaystyle{ R_1 \cdot R_2 }[/math]로 표기하기도 합니다.)
- [math]\displaystyle{ R^\star }[/math] (스타 클로저, Star Closure 또는 Kleene Closure): [math]\displaystyle{ R }[/math]이 나타내는 언어의 문자열을 0번 이상 반복하여 연결한 모든 문자열의 집합을 의미합니다. (예: [math]\displaystyle{ a^\star }[/math]는 [math]\displaystyle{ \epsilon, a, aa, aaa, \dots }[/math]를 포함합니다.)
괄호 (Parentheses):
- [math]\displaystyle{ (R) }[/math]: 정규 표현식 [math]\displaystyle{ R }[/math]과 동일한 언어를 나타내며, 연산의 우선순위를 명확히 하거나 그룹핑하는 데 사용됩니다.

정규 표현식으로 기술된 문자열의 집합은 정규 언어(regular language) 를 형성하며, 이는 유한 오토마타(finite automaton)에 의해 인식될 수 있는 형식 언어의 한 종류입니다.

정규 표현식의 의미 (Semantics)

정규 표현식 [math]\displaystyle{ R }[/math]의 의미는 [math]\displaystyle{ R }[/math]이 나타내는 언어, 즉 문자열의 집합 [math]\displaystyle{ L(R) }[/math]로 정의됩니다. [math]\displaystyle{ L(R) }[/math]은 항상 [math]\displaystyle{ \Sigma^\star }[/math]의 부분집합입니다.

[math]\displaystyle{ L(\emptyset) = \emptyset }[/math] (빈 집합)
[math]\displaystyle{ L(\epsilon) = \{ \epsilon\} }[/math] (빈 문자열만을 원소로 갖는 집합)
알파벳 기호 [math]\displaystyle{ a \in \Sigma }[/math]에 대해, [math]\displaystyle{ L(a) = \{ a\} }[/math] (문자열 [math]\displaystyle{ a }[/math]만을 원소로 갖는 집합)
[math]\displaystyle{ L(R_1 | R_2) = L(R_1) \cup L(R_2) }[/math] (두 언어의 합집합)
[math]\displaystyle{ L(R_1 R_2) = L(R_1)L(R_2) }[/math] (두 언어의 연결)
[math]\displaystyle{ L(R^\star) = (L(R))^\star }[/math] (언어 [math]\displaystyle{ L(R) }[/math]의 스타 클로저)
[math]\displaystyle{ L((R)) = L(R) }[/math] (괄호는 언어의 의미를 바꾸지 않음)

정규 정의 (Regular Definitions)

모든 명세를 기본적인 정규 표현식만으로 표현하는 것은 때때로 매우 번거롭고 가독성이 떨어질 수 있습니다. 정규 정의(Regular Definition)는 이러한 불편함을 해소하기 위해 정규 표현식에 이름을 부여하고, 이후 다른 정규 표현식에서 그 이름을 참조하여 사용할 수 있도록 하는 방법입니다.

형식적으로 정규 정의는 다음과 같은 형태의 정의들의 나열입니다: [math]\displaystyle{ d_1 \rightarrow r_1 }[/math] [math]\displaystyle{ d_2 \rightarrow r_2 }[/math] [math]\displaystyle{ \dots }[/math] [math]\displaystyle{ d_n \rightarrow r_n }[/math]

여기서 각 [math]\displaystyle{ d_i }[/math]는 새로운 이름(토큰 이름 등)이며, 알파벳 [math]\displaystyle{ \Sigma }[/math]에는 속하지 않는 기호여야 합니다 ([math]\displaystyle{ d_i \notin \Sigma }[/math]). 각 [math]\displaystyle{ r_i }[/math]는 알파벳 [math]\displaystyle{ \Sigma }[/math]와 이전에 정의된 이름들 [math]\displaystyle{ \{ d_1, d_2, \dots, d_{i-1}\} }[/math]을 사용하여 구성된 정규 표현식입니다.

예를 들어, 파스칼(Pascal) 언어의 식별자를 정의한다면 다음과 같이 할 수 있습니다:

letter_ [math]\displaystyle{ \rightarrow A | B | \dots | Z | a | b | \dots | z | }[/math] _ (밑줄 문자도 허용하는 경우) digit [math]\displaystyle{ \rightarrow 0 | 1 | \dots | 9 }[/math] id [math]\displaystyle{ \rightarrow }[/math] letter_ (letter_ | digit)*

여기서 letter_와 digit은 보조적인 이름이며, id가 최종적으로 식별자 토큰을 정의하는 이름이 됩니다.

정규 표현식의 확장 (Extensions of Regular Expressions)

가독성과 편의성을 위해 기본적인 정규 표현식 외에 다음과 같은 확장된 표기법들이 자주 사용됩니다:

양성 클로저 (Positive Closure) [math]\displaystyle{ R^+ }[/math]: [math]\displaystyle{ R }[/math]이 한 번 이상 반복되는 것을 의미합니다. 즉, [math]\displaystyle{ L(R^+) = L(R)^+ = L(R R^\star) = L(R^\star R) }[/math] 입니다.
선택적 발생 (Zero or One Instance) [math]\displaystyle{ R? }[/math]: [math]\displaystyle{ R }[/math]이 0번 또는 1번 발생하는 것을 의미합니다. 즉, [math]\displaystyle{ L(R?) = L(R) \cup \{ \epsilon\} }[/math] 입니다.
문자 클래스 (Character Classes) [a_1a_2...a_n]: [math]\displaystyle{ a_1 | a_2 | \dots | a_n }[/math]을 간략하게 표현한 것입니다. 예를 들어 [abc]는 a|b|c와 같습니다.
범위 지정 문자 클래스 [a_1-a_n]: 연속된 기호들을 나타냅니다. 예를 들어 [a-z]는 a|b|\dots|z와 같으며, 보통 알파벳 소문자 전체를 의미합니다. [0-9]는 숫자 하나를 의미합니다.

이러한 확장 표기법들은 기본적인 정규 표현식 연산들(선택, 연결, 스타 클로저)을 사용하여 모두 동등한 기본 정규 표현식으로 변환될 수 있습니다. 예를 들어, [math]\displaystyle{ R^+ = R R^\star }[/math] 이고, [math]\displaystyle{ R? = R | \epsilon }[/math] 입니다.

문자열 인식과 유한 오토마타 (String Recognition by Finite Automata)

정규 표현식으로 토큰의 패턴을 명세했다면, 다음 단계는 주어진 문자열이 해당 패턴에 속하는지, 즉 특정 정규 언어에 속하는지를 인식(recognize) 하는 메커니즘을 구현하는 것입니다. 이를 위해 유한 오토마타(Finite Automata, FA) 가 사용됩니다. 유한 오토마타는 정규 언어를 인식할 수 있는 가장 간단한 계산 모델입니다.

유한 오토마타에는 크게 두 가지 종류가 있습니다:

비결정적 유한 오토마타 (Nondeterministic Finite Automaton, NFA)
결정적 유한 오토마타 (Deterministic Finite Automaton, DFA)

어휘 분석기를 실제로 구현할 때는 주로 DFA를 사용하지만, 정규 표현식에서 오토마타를 구축하는 과정은 NFA를 중간 단계로 거치는 것이 더 쉽고 직관적입니다.

비결정적 유한 오토마타 (NFA)

NFA(Nondeterministic Finite Automaton) 는 입력 문자열에 대해 다음 상태가 유일하게 결정되지 않을 수 있는 유한 오토마타입니다. 즉, 특정 상태에서 같은 입력 기호에 대해 여러 다음 상태로 전이(transition)할 수 있거나, 입력 기호 없이도 ([math]\displaystyle{ \epsilon }[/math]-전이) 상태를 변경할 수 있습니다. NFA가 어떤 문자열을 받아들인다는 것은 그 문자열을 처리하는 여러 가능한 경로 중 하나라도 최종적으로 종료 상태(accepting state 또는 final state) 에 도달하는 경로가 존재한다는 의미입니다.

어휘 분석기를 구축하는 과정은 보통 다음과 같습니다:

정규 표현식으로 정의된 각 토큰 패턴을 NFA로 변환합니다 (예: 톰슨 구성법 사용).
생성된 NFA들을 (필요하다면) 하나로 결합합니다.
결합된 NFA를 이와 동등한 DFA로 변환합니다 (예: 부분집합 구성법 사용).

이 최종 DFA가 어휘 분석기에서 토큰을 인식하는 데 사용됩니다.

NFA의 정의

NFA는 5개의 구성요소로 이루어진 튜플(tuple) [math]\displaystyle{ M = (Q, \Sigma, \delta, q_0, F) }[/math]로 정의됩니다:

[math]\displaystyle{ Q }[/math]: 유한한 상태(state) 들의 집합입니다.
[math]\displaystyle{ \Sigma }[/math]: 유한한 입력 기호(input symbol) 들의 집합, 즉 입력 알파벳(input alphabet) 입니다. [math]\displaystyle{ \epsilon }[/math] (빈 문자열)은 입력 알파벳에 포함되지 않는다고 가정합니다 ([math]\displaystyle{ \epsilon \notin \Sigma }[/math]).
[math]\displaystyle{ \delta }[/math]: 전이 함수(transition function) 이며, [math]\displaystyle{ Q \times (\Sigma \cup \{ \epsilon\}) \rightarrow 2^Q }[/math] 형태를 가집니다. 즉, 특정 상태에서 특정 입력 기호(또는 [math]\displaystyle{ \epsilon }[/math])를 받았을 때, 전이할 수 있는 다음 상태들의 집합(멱집합 [math]\displaystyle{ 2^Q }[/math]의 원소)을 반환합니다. 이것이 NFA의 비결정성을 나타내는 핵심 부분입니다. (예를 들어, [math]\displaystyle{ Q = \{ q_0, q_1, q_2\} }[/math]일 때, [math]\displaystyle{ 2^Q = \{ \emptyset, \{ q_0\}, \{ q_1\}, \{ q_2\}, \{ q_0, q_1\}, \{ q_0, q_2\}, \{ q_1, q_2\}, \{ q_0, q_1, q_2\}\} }[/math] 입니다.)
[math]\displaystyle{ q_0 \in Q }[/math]: 초기 상태(initial state) 입니다.
[math]\displaystyle{ F \subseteq Q }[/math]: 종료 상태(final state 또는 accepting state) 들의 집합입니다. 이 상태들 중 하나에서 입력 문자열 처리가 끝나면 해당 문자열은 NFA에 의해 인식(수용)됩니다.

결정적 유한 오토마타 (DFA)

DFA(Deterministic Finite Automaton) 는 NFA의 특별한 경우로, 다음과 같은 두 가지 주요 특징을 가집니다:

[math]\displaystyle{ \epsilon }[/math]-전이가 없습니다. 즉, 입력 기호 없이 상태를 변경할 수 없습니다.
각 상태와 각 입력 기호에 대해, 다음으로 전이할 상태가 유일하게 하나로 결정됩니다.

이러한 결정성 때문에 DFA는 문자열을 인식하는 알고리즘을 구현하기에 더 직접적이고 효율적입니다. 어휘 분석기의 실제 실행 엔진은 주로 DFA 형태로 구현됩니다.

DFA의 정의

DFA 또한 5개의 구성요소로 이루어진 튜플 [math]\displaystyle{ M = (Q, \Sigma, \delta, q_0, F) }[/math]로 정의됩니다:

[math]\displaystyle{ Q }[/math]: 유한한 상태(state) 들의 집합입니다.
[math]\displaystyle{ \Sigma }[/math]: 유한한 입력 기호(input symbol) 들의 집합 (입력 알파벳)입니다.
[math]\displaystyle{ \delta }[/math]: 전이 함수(transition function) 이며, [math]\displaystyle{ Q \times \Sigma \rightarrow Q }[/math] 형태를 가집니다. 즉, 특정 상태에서 특정 입력 기호를 받았을 때, 다음 상태가 단 하나 로 결정됩니다. (NFA와 달리 [math]\displaystyle{ 2^Q }[/math]가 아닌 [math]\displaystyle{ Q }[/math]로 매핑됩니다.) 이 함수는 모든 상태와 모든 입력 기호의 쌍에 대해 정의된 전체 함수(total function)여야 합니다. (만약 특정 입력에 대한 전이가 없다면, 보통 오류 상태 또는 "죽은 상태(dead state)"로 가는 전이가 있다고 가정합니다.)
[math]\displaystyle{ q_0 \in Q }[/math]: 초기 상태(initial state) 입니다.
[math]\displaystyle{ F \subseteq Q }[/math]: 종료 상태(final state) 들의 집합입니다.

자동화 (Automation): 정규 표현식에서 DFA까지

지금까지 정규 표현식으로 어휘 패턴을 명세하고, 유한 오토마타(NFA, DFA)로 이를 인식하는 방법을 살펴보았습니다. 실제 어휘 분석기를 개발할 때는 이러한 변환 과정을 자동화하는 도구를 사용합니다. 이 자동화 과정은 일반적으로 다음의 두 주요 단계를 거칩니다:

정규 표현식(RE) [math]\displaystyle{ \rightarrow }[/math] NFA 변환: 각 정규 표현식을 그와 동등한 NFA로 변환합니다. (예: 톰슨 구성법 (Thompson's Construction))
NFA [math]\displaystyle{ \rightarrow }[/math] DFA 변환: 생성된 NFA(또는 여러 NFA를 결합한 NFA)를 이와 동등한 DFA로 변환합니다. (예: 부분집합 구성법 (Subset Construction))

톰슨 구성법 (Thompson's Construction): RE [math]\displaystyle{ \rightarrow }[/math] NFA

톰슨 구성법은 정규 표현식의 구조에 따라 재귀적으로 NFA를 구축하는 알고리즘입니다. 이 방법의 핵심 원리는 다음과 같습니다:

합성성(Compositionality): 복잡한 정규 표현식에 대한 NFA는 그보다 단순한 부분 정규 표현식들에 대한 NFA들을 결합하여 만듭니다.
불변 조건(Invariants): 구성되는 각 NFA 조각(fragment)은 다음과 같은 불변 조건을 만족하도록 설계됩니다:
- 단 하나의 종료 상태(accepting state) 만을 가집니다.
- 초기 상태(initial state)로 들어오는 전이(arc)가 없습니다.
- 종료 상태에서 나가는 전이가 없습니다.

이러한 불변 조건 덕분에 작은 NFA 조각들을 새로운 초기 상태와 종료 상태를 추가하고 [math]\displaystyle{ \epsilon }[/math]-전이를 이용하여 쉽게 결합할 수 있습니다.

톰슨 구성법의 기본 단계 (Base Cases and Inductive Steps)

톰슨 구성법은 정규 표현식의 기본 요소와 연산에 대해 NFA를 구성하는 방법을 정의합니다.

1. 정규 표현식 [math]\displaystyle{ R = \epsilon }[/math] (빈 문자열):

새로운 초기 상태 [math]\displaystyle{ i }[/math]와 새로운 종료 상태 [math]\displaystyle{ f }[/math]를 만들고, [math]\displaystyle{ i }[/math]에서 [math]\displaystyle{ f }[/math]로 가는 [math]\displaystyle{ \epsilon }[/math]-전이를 추가합니다. [math]\displaystyle{ L(N(R)) = \{ \epsilon\} }[/math]

2. 정규 표현식 [math]\displaystyle{ R = a }[/math] (알파벳 [math]\displaystyle{ \Sigma }[/math]에 속하는 단일 기호):

새로운 초기 상태 [math]\displaystyle{ i }[/math]와 새로운 종료 상태 [math]\displaystyle{ f }[/math]를 만들고, [math]\displaystyle{ i }[/math]에서 [math]\displaystyle{ f }[/math]로 가는 입력 기호 [math]\displaystyle{ a }[/math]에 대한 전이를 추가합니다. [math]\displaystyle{ L(N(R)) = \{ a\} }[/math]

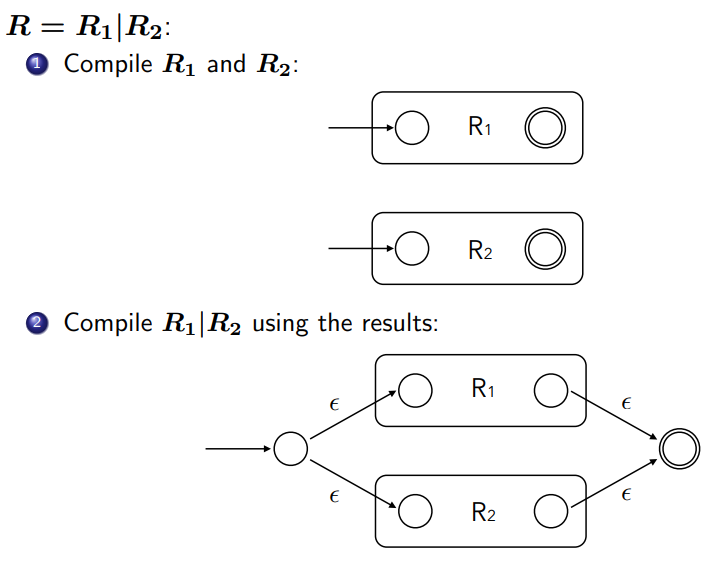
3. 정규 표현식 [math]\displaystyle{ R = R_1 | R_2 }[/math] (선택, Alternation):

[math]\displaystyle{ R_1 }[/math]에 대한 NFA [math]\displaystyle{ N(R_1) }[/math]과 [math]\displaystyle{ R_2 }[/math]에 대한 NFA [math]\displaystyle{ N(R_2) }[/math]를 먼저 구성합니다.

새로운 초기 상태 [math]\displaystyle{ i }[/math]와 새로운 종료 상태 [math]\displaystyle{ f }[/math]를 만듭니다.

[math]\displaystyle{ i }[/math]에서 [math]\displaystyle{ N(R_1) }[/math]의 초기 상태로 [math]\displaystyle{ \epsilon }[/math]-전이를 추가합니다.
[math]\displaystyle{ i }[/math]에서 [math]\displaystyle{ N(R_2) }[/math]의 초기 상태로 [math]\displaystyle{ \epsilon }[/math]-전이를 추가합니다.
[math]\displaystyle{ N(R_1) }[/math]의 종료 상태에서 [math]\displaystyle{ f }[/math]로 [math]\displaystyle{ \epsilon }[/math]-전이를 추가합니다.
[math]\displaystyle{ N(R_2) }[/math]의 종료 상태에서 [math]\displaystyle{ f }[/math]로 [math]\displaystyle{ \epsilon }[/math]-전이를 추가합니다.

[math]\displaystyle{ L(N(R)) = L(N(R_1)) \cup L(N(R_2)) }[/math]

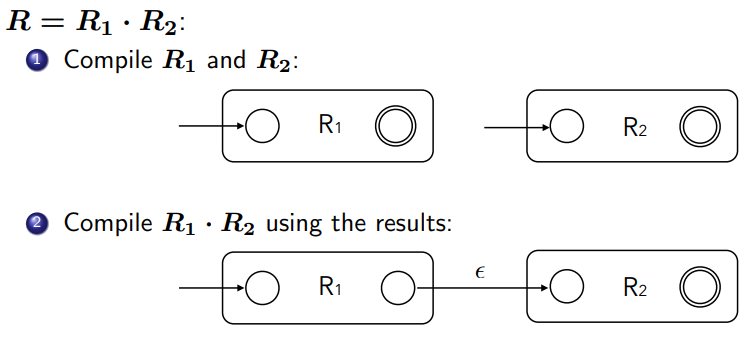
4. 정규 표현식 [math]\displaystyle{ R = R_1 R_2 }[/math] (연결, Concatenation):

[math]\displaystyle{ R_1 }[/math]에 대한 NFA [math]\displaystyle{ N(R_1) }[/math]과 [math]\displaystyle{ R_2 }[/math]에 대한 NFA [math]\displaystyle{ N(R_2) }[/math]를 먼저 구성합니다.

[math]\displaystyle{ N(R_1) }[/math]의 초기 상태가 [math]\displaystyle{ N(R) }[/math]의 초기 상태가 됩니다.

[math]\displaystyle{ N(R_1) }[/math]의 종료 상태를 [math]\displaystyle{ N(R_2) }[/math]의 초기 상태와 [math]\displaystyle{ \epsilon }[/math]-전이로 (또는 직접 상태를 합쳐서) 연결합니다.

[math]\displaystyle{ N(R_2) }[/math]의 종료 상태가 [math]\displaystyle{ N(R) }[/math]의 종료 상태가 됩니다.

[math]\displaystyle{ L(N(R)) = L(N(R_1)) L(N(R_2)) }[/math]

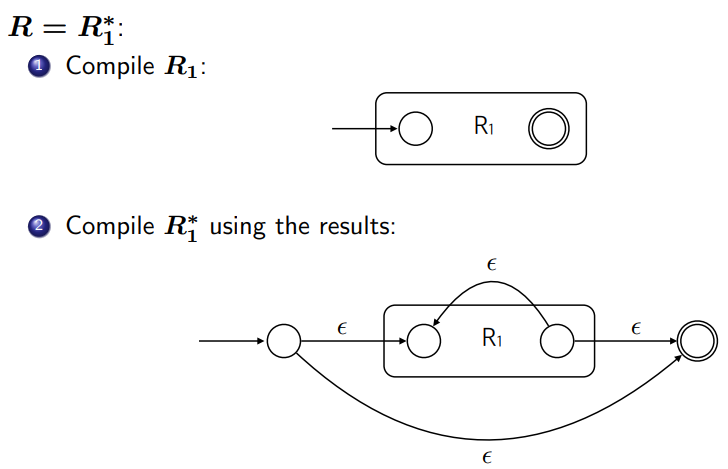
5. 정규 표현식 [math]\displaystyle{ R = R_1^\star }[/math] (스타 클로저, Kleene Closure):

[math]\displaystyle{ R_1 }[/math]에 대한 NFA [math]\displaystyle{ N(R_1) }[/math]을 먼저 구성합니다. 새로운 초기 상태 [math]\displaystyle{ i }[/math]와 새로운 종료 상태 [math]\displaystyle{ f }[/math]를 만듭니다.

[math]\displaystyle{ i }[/math]에서 [math]\displaystyle{ f }[/math]로 [math]\displaystyle{ \epsilon }[/math]-전이를 추가합니다 (0번 반복을 위함).
[math]\displaystyle{ i }[/math]에서 [math]\displaystyle{ N(R_1) }[/math]의 초기 상태로 [math]\displaystyle{ \epsilon }[/math]-전이를 추가합니다.
[math]\displaystyle{ N(R_1) }[/math]의 종료 상태에서 [math]\displaystyle{ f }[/math]로 [math]\displaystyle{ \epsilon }[/math]-전이를 추가합니다.
[math]\displaystyle{ N(R_1) }[/math]의 종료 상태에서 [math]\displaystyle{ N(R_1) }[/math]의 초기 상태로 [math]\displaystyle{ \epsilon }[/math]-전이를 추가합니다 (1번 이상 반복을 위함).

[math]\displaystyle{ L(N(R)) = (L(N(R_1)))^\star }[/math]

(참고: [math]\displaystyle{ R = \emptyset }[/math] 에 대한 NFA는 시작 상태와 도달 불가능한 종료 상태, 또는 종료 상태가 없는 형태로 구성하여 어떤 문자열도 받아들이지 않도록 합니다.)

부분집합 구성법 (Subset Construction): NFA [math]\displaystyle{ \rightarrow }[/math] DFA

톰슨 구성법으로 얻은 NFA는 비결정성과 [math]\displaystyle{ \epsilon }[/math]-전이 때문에 직접 어휘 분석기로 사용하기에는 비효율적일 수 있습니다. 따라서 이를 효율적인 DFA로 변환하는 과정이 필요하며, 이때 부분집합 구성법(Subset Construction) 알고리즘이 사용됩니다.

부분집합 구성법의 핵심 아이디어는 DFA의 각 상태가 NFA 상태들의 부분집합에 해당하도록 만드는 것입니다. 즉, DFA의 한 상태는 NFA에서 동시에 존재할 수 있는 여러 상태의 모음을 나타냅니다.

[math]\displaystyle{ \epsilon }[/math]-클로저 ([math]\displaystyle{ \epsilon }[/math]-Closure)

부분집합 구성법을 이해하기 위해서는 먼저 [math]\displaystyle{ \epsilon }[/math]-클로저 개념을 알아야 합니다. NFA 상태들의 집합 [math]\displaystyle{ I }[/math]에 대한 [math]\displaystyle{ \epsilon\text{-Closure}(I) }[/math]는 [math]\displaystyle{ I }[/math]에 속한 임의의 상태 [math]\displaystyle{ s }[/math]에서 출발하여 [math]\displaystyle{ \epsilon }[/math]-전이만을 0번 이상 따라갔을 때 도달할 수 있는 모든 NFA 상태들의 집합입니다.

[math]\displaystyle{ \epsilon\text{-Closure}(I) }[/math] 계산 알고리즘 (정의):

[math]\displaystyle{ \epsilon\text{-closure}(I) }[/math]는 다음 두 조건을 만족하는 가장 작은 NFA 상태 집합 [math]\displaystyle{ T }[/math]입니다:

기본 경우(Base Case): [math]\displaystyle{ I }[/math]에 속한 모든 상태는 [math]\displaystyle{ T }[/math]에 포함됩니다 (즉, [math]\displaystyle{ I \subseteq T }[/math]).
귀납적 단계(Inductive Step): 만약 상태 [math]\displaystyle{ s }[/math]가 [math]\displaystyle{ T }[/math]에 있고, [math]\displaystyle{ s }[/math]에서 상태 [math]\displaystyle{ s' }[/math]로 가는 [math]\displaystyle{ \epsilon }[/math]-전이 (즉, [math]\displaystyle{ s' \in \delta_{NFA}(s, \epsilon) }[/math])가 존재한다면, [math]\displaystyle{ s' }[/math] 또한 [math]\displaystyle{ T }[/math]에 포함됩니다.

이 집합 [math]\displaystyle{ T }[/math]는 [math]\displaystyle{ I }[/math]에 있는 임의의 상태에서 [math]\displaystyle{ \epsilon }[/math]-전이만을 0번 이상 따라 도달할 수 있는 모든 상태를 포함합니다. [math]\displaystyle{ T }[/math]가 [math]\displaystyle{ I }[/math]에서 시작하는 [math]\displaystyle{ \epsilon }[/math]-전이에 대해 닫혀있는(closed) 가장 작은 집합이라는 속성은 다음 조건으로도 특징지을 수 있습니다: 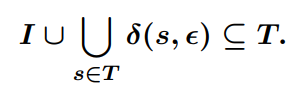이는 [math]\displaystyle{ T }[/math]가 반드시 [math]\displaystyle{ I }[/math]를 포함해야 하며, 이미 [math]\displaystyle{ T }[/math]에 있는 어떤 상태에서든 단일 [math]\displaystyle{ \epsilon }[/math]-이동으로 도달할 수 있는 모든 상태 또한 [math]\displaystyle{ T }[/math]의 일부여야 함을 의미합니다 (이는 [math]\displaystyle{ T }[/math]를 넘어서는 더 이상의 확장이 불가능함을 암시합니다).

[math]\displaystyle{ \epsilon\text{-Closure}(I) }[/math] 계산 알고리즘 (최소 고정점):

함수 [math]\displaystyle{ F(X) = I \cup \{ s' \mid s \in X \text{ and } s' \in \delta_{NFA}(s, \epsilon)\} }[/math]를 정의할 수 있습니다. (이 함수는 집합 [math]\displaystyle{ I }[/math]와 집합 [math]\displaystyle{ X }[/math]의 상태들로부터 단일 [math]\displaystyle{ \epsilon }[/math]-단계로 도달 가능한 모든 상태들을 계산합니다.) 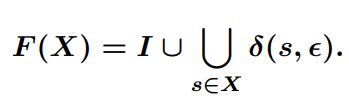그러면 [math]\displaystyle{ \epsilon\text{-closure}(I) }[/math]는 [math]\displaystyle{ T = F(T) }[/math] 방정식을 만족하는 가장 작은 집합 [math]\displaystyle{ T }[/math]입니다. 이 해 [math]\displaystyle{ T }[/math]를 [math]\displaystyle{ F }[/math]의 최소 고정점(least fixed point)이라고 부릅니다. 이 최소 고정점은 아래 제시된 반복 알고리즘처럼 [math]\displaystyle{ F }[/math]를 반복적으로 적용하여 찾을 수 있습니다.

[math]\displaystyle{ \epsilon\text{-Closure}(I) }[/math] 계산을 위한 반복 알고리즘:

T = I;
WorkList = I; // 처리할 상태들을 담는 작업 목록
while WorkList is not empty do
    remove some state s from WorkList;
    for each state s' such that s' ∈ δ_NFA(s, ε) do // s에서 s'로 가는 모든 ε-전이에 대해
        if s' is not in T then
            add s' to T;
            add s' to WorkList;
        end if
    end for
end while
return T;

부분집합 구성 알고리즘 (Subset Construction Algorithm)

DFA의 각 상태 [math]\displaystyle{ d }[/math]는 NFA 상태들의 집합 [math]\displaystyle{ S }[/math]에 대해 [math]\displaystyle{ d = \epsilon\text{-closure}(S) }[/math]로 표현됩니다. 알고리즘은 다음과 같이 진행됩니다:

초기 상태 계산: DFA의 초기 상태 [math]\displaystyle{ d_0 }[/math]는 NFA의 초기 상태 [math]\displaystyle{ q_0 }[/math]에 대한 [math]\displaystyle{ \epsilon\text{-closure}(\{ q_0\}) }[/math] 입니다. [math]\displaystyle{ d_0 }[/math]를 DFA 상태 집합 [math]\displaystyle{ Q_D }[/math]에 추가하고, 처리해야 할 상태 목록(예: 워크리스트 [math]\displaystyle{ W }[/math])에 추가합니다.
반복: 워크리스트 [math]\displaystyle{ W }[/math]가 비어있지 않은 동안 다음을 반복합니다:
1. [math]\displaystyle{ W }[/math]에서 DFA 상태 [math]\displaystyle{ q_D }[/math] (NFA 상태들의 집합임)를 하나 꺼냅니다.
2. 입력 알파벳 [math]\displaystyle{ \Sigma }[/math]의 각 기호 [math]\displaystyle{ c }[/math]에 대해 다음을 수행합니다:
  1. [math]\displaystyle{ \text{move}(q_D, c) = \bigcup_{s \in q_D} \delta_{NFA}(s, c) }[/math]. 즉, [math]\displaystyle{ q_D }[/math]에 속한 모든 NFA 상태에서 입력 [math]\displaystyle{ c }[/math]를 따라 전이할 수 있는 NFA 상태들의 집합을 구합니다.
  2. [math]\displaystyle{ t_D = \epsilon\text{-closure}(\text{move}(q_D, c)) }[/math]. 이 [math]\displaystyle{ t_D }[/math]가 [math]\displaystyle{ q_D }[/math]에서 [math]\displaystyle{ c }[/math] 입력을 받았을 때 전이할 다음 DFA 상태입니다.
  3. [math]\displaystyle{ \delta_{DFA}(q_D, c) = t_D }[/math]로 DFA의 전이 함수를 정의합니다.
  4. 만약 [math]\displaystyle{ t_D }[/math]가 [math]\displaystyle{ Q_D }[/math]에 새롭게 추가된 상태라면, [math]\displaystyle{ t_D }[/math]를 [math]\displaystyle{ W }[/math]에도 추가합니다.
종료 상태 결정: DFA 상태 [math]\displaystyle{ q_D \in Q_D }[/math]가 종료 상태가 되는 조건은, [math]\displaystyle{ q_D }[/math]에 포함된 NFA 상태들 중 적어도 하나가 NFA의 종료 상태([math]\displaystyle{ N_A }[/math])인 경우입니다. 즉, [math]\displaystyle{ F_D = \{ q_D \in Q_D \mid q_D \cap N_A \ne \emptyset\} }[/math] 입니다.

부분집합 구성 실행 예제 (Running Example)

이 예제는 부분집합 구성 알고리즘이 NFA를 DFA로 어떻게 변환하는지 보여줍니다. 여기서 사용되는 (명시적으로 그려지진 않았지만 가정된) NFA는 다음과 같은 특징을 가진다고 가정합니다:

상태 집합 [math]\displaystyle{ Q_{NFA} }[/math]는 [math]\displaystyle{ \{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, \dots\} }[/math]를 포함합니다.
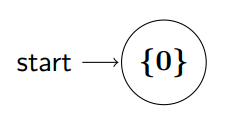
상태 [math]\displaystyle{ \{ 0\} }[/math]은 이 NFA의 시작 상태입니다.
입력 알파벳 [math]\displaystyle{ \Sigma = \{ a, b, c\} }[/math] 입니다.
NFA의 전이 함수 [math]\displaystyle{ \delta_{NFA} }[/math]와 [math]\displaystyle{ \epsilon }[/math]-전이는 아래 단계에서 보여지는 결과를 도출합니다.

목표는 DFA [math]\displaystyle{ D = (Q_{DFA}, \Sigma, \delta_{DFA}, d_0, F_{DFA}) }[/math]를 구성하는 것입니다.

초기 DFA 상태 [math]\displaystyle{ d_0 }[/math]:

DFA의 초기 상태 [math]\displaystyle{ d_0 }[/math]는 NFA 시작 상태의 [math]\displaystyle{ \epsilon\text{-closure} }[/math]입니다. NFA 시작 상태를 [math]\displaystyle{ q_0 = \{0\} }[/math]이라 하고, 이 상태에서 다른 상태로 가는 [math]\displaystyle{ \epsilon }[/math]-전이가 없어 확장되지 않는다고 가정하면: [math]\displaystyle{ d_0 = \epsilon\text{-closure}(\{ 0\}) = \{ 0\} }[/math]

[math]\displaystyle{ d_0 }[/math] (즉, [math]\displaystyle{ S = \{ 0\} }[/math])로부터의 전이 계산:

[math]\displaystyle{ d_0 = \{ 0\} }[/math]과 각 입력 [math]\displaystyle{ x \in \Sigma }[/math]에 대해 [math]\displaystyle{ \delta_{DFA}(d_0, x) = \epsilon\text{-closure}(\text{move}(d_0, x)) }[/math]를 계산합니다. [math]\displaystyle{ \text{move}(S', \text{input}) = \bigcup_{s \in S'} \delta_{NFA}(s, \text{input}) }[/math]입니다.

일반적인 계산 단계는 다음 이미지의 수식으로 표현됩니다:

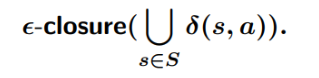
입력 'a':

[math]\displaystyle{ S = \{ 0\} }[/math]이므로 [math]\displaystyle{ \text{move}(\{ 0\}, a) = \bigcup_{s \in \{ 0\}} \delta_{NFA}(s, a) }[/math]를 계산합니다. 예제에 따르면, [math]\displaystyle{ \epsilon\text{-closure}(\bigcup_{s \in \{ 0\}} \delta_{NFA}(s, a)) = \{ 1, 2, 3, 4, 6, 9\} }[/math]입니다. 이 새로운 DFA 상태를 [math]\displaystyle{ d_1 = \{ 1, 2, 3, 4, 6, 9\} }[/math]라고 하면, [math]\displaystyle{ \delta_{DFA}(\{ 0\}, a) = d_1 }[/math]입니다.

입력 'b':

예제에 따르면, [math]\displaystyle{ \epsilon\text{-closure}(\bigcup_{s \in \{ 0\}} \delta_{NFA}(s, b)) = \emptyset }[/math]입니다. 이는 [math]\displaystyle{ \text{move}(\{ 0\}, b) }[/math]가 [math]\displaystyle{ \emptyset }[/math]이었음을 의미합니다. 따라서 [math]\displaystyle{ \delta_{DFA}(\{ 0\}, b) = \emptyset }[/math]입니다. (이는 DFA에서 "죽은 상태"로의 전이를 의미하거나, 전이가 정의되지 않았음을 나타낼 수 있습니다.)

입력 'c':

예제에 따르면, [math]\displaystyle{ \epsilon\text{-closure}(\bigcup_{s \in \{ 0\}} \delta_{NFA}(s, c)) = \emptyset }[/math]입니다. 따라서 [math]\displaystyle{ \delta_{DFA}(\{ 0\}, c) = \emptyset }[/math]입니다.

새로운 DFA 상태(예: [math]\displaystyle{ d_1 = \{ 1, 2, 3, 4, 6, 9\} }[/math])로부터의 전이 계산:

새로운 (아직 처리되지 않은) DFA 상태 [math]\displaystyle{ d_1 = \{ 1, 2, 3, 4, 6, 9\} }[/math]에 대해 각 입력 [math]\displaystyle{ x \in \Sigma }[/math]에 대한 전이를 계산합니다.

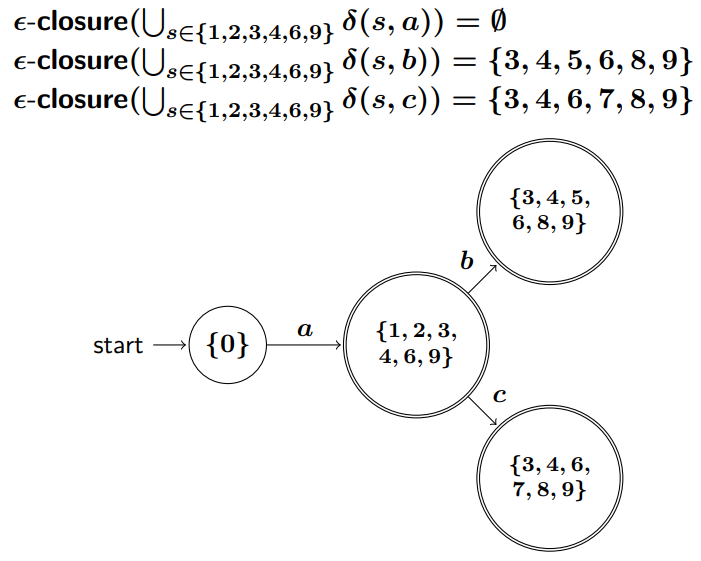
[math]\displaystyle{ d_1 }[/math]에서 입력 'a':

예제에 따르면, [math]\displaystyle{ \epsilon\text{-closure}(\bigcup_{s \in \{ 1,2,3,4,6,9\}} \delta_{NFA}(s, a)) = \emptyset }[/math]. 따라서 [math]\displaystyle{ \delta_{DFA}(d_1, a) = \emptyset }[/math].

[math]\displaystyle{ d_1 }[/math]에서 입력 'b':

예제에 따르면, [math]\displaystyle{ \epsilon\text{-closure}(\bigcup_{s \in \{ 1,2,3,4,6,9\}} \delta_{NFA}(s, b)) = \{ 3, 4, 5, 6, 8, 9\} }[/math]. 이 새로운 DFA 상태를 [math]\displaystyle{ d_2 = \{ 3, 4, 5, 6, 8, 9\} }[/math]라고 하면, [math]\displaystyle{ \delta_{DFA}(d_1, b) = d_2 }[/math].

[math]\displaystyle{ d_1 }[/math]에서 입력 'c':

예제에 따르면, [math]\displaystyle{ \epsilon\text{-closure}(\bigcup_{s \in \{ 1,2,3,4,6,9\}} \delta_{NFA}(s, c)) = \{ 3, 4, 6, 7, 8, 9\} }[/math]. 이 새로운 DFA 상태를 [math]\displaystyle{ d_3 = \{ 3, 4, 6, 7, 8, 9\} }[/math]라고 하면, [math]\displaystyle{ \delta_{DFA}(d_1, c) = d_3 }[/math].

이러한 과정은 새로운 DFA 상태가 더 이상 생성되지 않을 때까지 반복됩니다. 어떤 DFA 상태 [math]\displaystyle{ d_i }[/math]가 NFA의 종료 상태를 하나라도 포함하고 있다면, 그 DFA 상태 [math]\displaystyle{ d_i }[/math]는 DFA의 종료 상태가 됩니다.